Frans van Schooten presenteert op bladzijde 126 een constructie om een lijnstuk middendoor te delen. Deze constructie kan met één extra lijn uitgebreid worden tot een constructie om een derde deel van een lijn te bepalen. Nadat F bepaald is, kan G bepaald worden uit CF = FG. Tussen C en D ligt H met AC = CH = DH want CD is twee maal AC. De lijn GH snijdt lijn AB in I met AI twee keer zo groot als BI. Lijnstuk BI is dan een derde deel van lijnstuk AB.

Het bewijs dat deze constructie correct is, maakt gebruik van het feit dat ∆GBE een vergroting is van ∆CDE met vergrotingsfactor 2. Gelijk zijn ∆CHG en ∆GBE want ∠GCD = ∠EGB en CG = GE en GB = CH. Dus is HG even groot als BD. Vierhoek HDBG is dan een parallellogram vanwege de even lange overstaande zijden: HG = BE = BD en GB = CH = HD. Dat betekent dat BD en HG evenwijdig zijn.
Gevolg is dat ∆ABD en ∆AIH een vergroting van elkaar zijn met gelijke F-hoeken: ∠ADB = ∠AHI en ∠ABD = ∠AIH. De vergrotingsfactor is 2/3 en dus is AI twee-derde van AB. Dat betekent dat BI een-derde is van AB.
Daarmee is bewezen dat deze constructie een lijn verdeelt in de verhouding een-derde om twee-derde.

Tot slot een opmerking over lijn EH. Lijn EH snijdt AB, maar niet in een vaste verhouding als twee-derde om een-derde en ook niet in de verhouding drie-kwart om een-kwart.

top

Een soortgelijke constructie kan gebruikt worden om een lijnstuk in andere verhoudingen te delen dan half om half, bijvoorbeeld in één-derde op twee-derde of een-kwart op drie-kwart. Als CD geconstrueerd wordt als een even veelvoud van AC, dan is BG een geheel veelvoud van AC, namelijk de helft van dat even veelvoud. Dit veelvoud dat BG is van AC is de vergrotingsfactor van ∆BEF ten opzichte van ∆ACF.

Een getallen voorbeeld laat zien wat er gebeurt.
Als CD = 6 × AC, dan is BG = 3 × AC, en dus is BF = 3 × AF, en dus is AF een-kwart van AB.
Op dezelfde manier.
Als CD = 12 × AC, dan is BG = 6 × AC, en dus is BF = 6 × AF, en dus is AF een-zevende van AB.

top

Een variatie op bladzijde 122 levert een constructie op om een lijnstuk in een willekeurige verhouding te delen.
Gegeven een lijnstuk dat verdeeld moet worden en gegeven twee andere lijnstukken die aangeven hoe. Opdracht is om het eerste lijnstuk zodanig te verdelen dat de verhouding tussen de lengte van beide delen gelijk is aan de verhouding tussen de lengtes van die twee andere gegeven lijnstukken.

De deellijn heeft een bijzondere eigenschap. Een deellijn deelt de overstaande zijde in de verhouding van de aanliggende zijden.

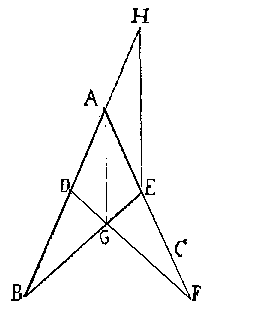
Gegeven BE, het lijnstuk dat verdeeld wordt, en AB en BE die de verhouding aangeven. In ∆ABE is AG de deellijn uit A. Te bewijzen is dat AB in dezelfde verhouding staat tot AE als BG staat tot EG.

Om dat te bewijzen is in de constructie AD verlengd tot AH waarbij EH evenwijdig is aan AG. Daarom is ∠EAG = ∠AEH. Omdat ∠DAG = ∠EAG en ∠EAH de overstaande, is ook ∠AEH = ∠AHE. Gevolg is dat ∆AEH gelijkbenig is. Vanwege de evenwijdigheid, zijn ∆ABG en ∆HBE gelijkhoekig. Ze zijn dus een vergroting van elkaar en dat betekent dat AB zich verhoudt tot BG als BH tot EB, maar ook als AH tot EG en omdat AH = AE ook als AE tot EG.

Conclusie is dat BE door de bissectrice AG verdeeld is in twee delen, BG en EG, en dat hun lengtes zich verhouden als AB tot AE.

top

top