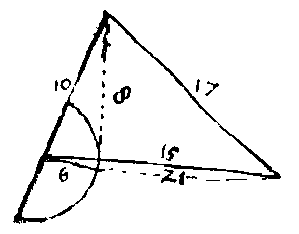|
 
De hoogtelijn in een driehoek met zijden 10 en 17 en 21 verdeelt de basis in 6 en 15.
De hoogtelijn in een driehoek met zijden 17 en 19 en 20 verdeelt de basis NIET in 10 en 10,
maar de zwaartelijn wel.
De zwaartelijn verdeelt per definitie de zijde van deze driehoek in twee evenlange delen.
Deze zwaartelijn is exact 15.
De hoogtelijn in een driehoek met zijden 17 en 19 en 30 verdeelt de basis NIET in 15 en 15,
maar de zwaartelijn wel.
Deze zwaartelijn is echter niet exact 12, maar exact 10!
|
|
Rechthoekige driehoeken met zijde 60:
| 60 | 11 | 61 | wordt niet genoemd
| | 60 | 17,5 | 62,5 | dat is 2,5 keer 7 24 25
| | 60 | 25 | 65 | dat is 5 keer 5 12 13
| | 60 | 32 | 68 | dat is 4 keer 8 15 17
| | 60 | 45 | 75 | dat is 15 keer 3 4 5
| | 60 | 63 | 87 | dat is 3 keer 20 21 29
| | 60 | 80 | 100 | dat is 20 keer 3 4 5
| | 60 | 91 | 109 | wordt niet genoemd
| | 60 | 144 | 156 | dat is 12 keer 5 12 13
| | 60 | 175 | 185 | dat is 5 keer 12 35 37
| | 60 | 2055/7 | 214²/7 | wordt niet genoemd
| | 60 | 221 | 229 | wordt niet genoemd
| | 60 | 297 | 303 | dat is 3 keer 20 99 101
| | 60 | 448 | 452 | dat is 4 keer 15 112 113
wordt niet genoemd
| | 60 | 899 | 901
|
Zwaartelijnen
Tussen de driehoeken staat de naam van Bachet en de afkorting Dioph. en "p 418".
Dat is een verwijzing naar de Franse wiskundige Claude Gaspard Bachet de Méziriac (1581-1638) die in 1621 een vertaling in het Latijn van de Arithmetica van Diophantus publiceerde. Diophantus is een Griekse wiskundige, afkomstig uit Alexandrië, uit de eerste eeuwen na de jaartelling. Op bladzijde 418 van dat boek wordt inderdaad gerekend aan zwaartelijnen.
Beide voorbeelden staan daar uitgewerkt: de driehoek met zijden 19, 17, 20 en hoogtelijn 15 en de driehoek met zijden 19, 17, 30 en hoogtelijn 12. Het lijkt erop dat Frans van Schooten het niet heeft nagerekend!
 Diophante Arithmeticorum libri sex
Mathematische Oeffeningen
Op 47 recto staat weer een verwijzing naar Bachet.
In GN439 heeft Frans van Schooten Junior een uitreksel geschreven.
|