Welcome to the Overwhelming Beauty of a Muqarnas
|
Welcome to Henk Hietbrink's webpage on muqarnas.
Muqarnas are a masterpiece of Islamic geometrical ornamentation. I call it works of art because it is so much more than geometry, although some mathematics can help to describe their structure.
For a true understanding, I recommend that we listen to the architects and engineerings who take care of their heritage.
For more information, please contact h.hietbrink planet.nl. planet.nl.
|
This webpage:
|
|
- Works of Art
Muqarnas are Works of Art |  |
- Aim of my Research
My research aims to develop algorithms that facilitate the transformation of 2D tessellated floor plans into 3D-printed muqarnas scale models by assigning standardized, pre-designed units. | 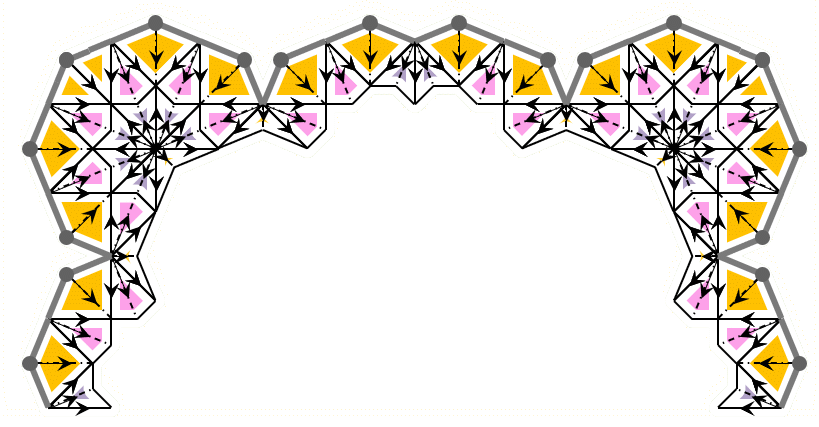 |
- From 2D to 3D: Bridging the Gap
The projection of a 3D muqarnas onto a plane forms a type of tessellation. However, a projection inherently contains less information than the original 3D structure, making it unclear whether a 2D tessellation can fully determine its 3D counterpart. |  |
- Read your Literature
Over the past fifty years, leading architects and scholars in Türkiye and Iran have published significant scholarly works on muqarnas. |  |
|
- Excel
Excel is my development environment to generate and analyze muqarnas floorplans. | 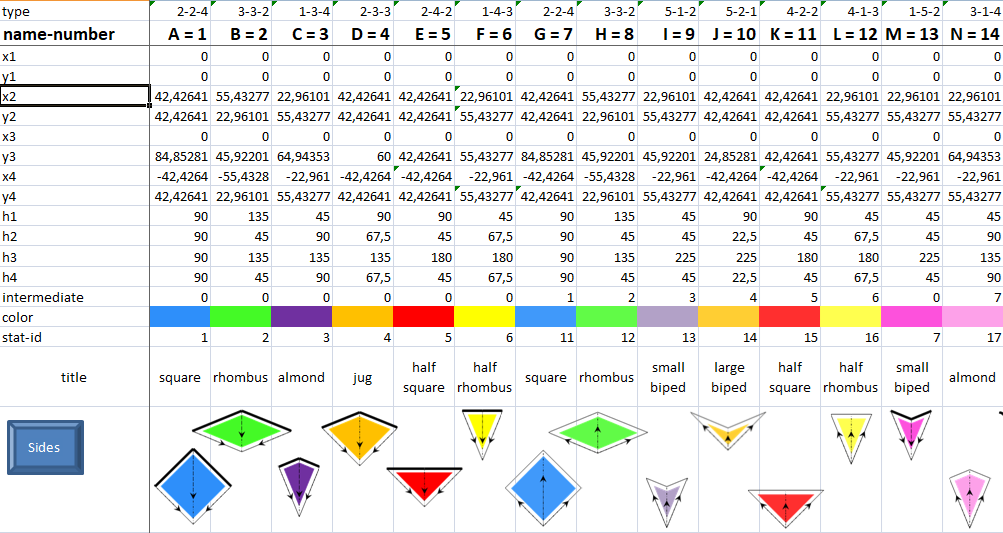 |
- GeoGebra
GeoGebra is a browserbased app in the cloud. GeoGebra's ability to define and modify macros is a powerful feature. It allows users to record macros and refine them later.
Together with Chris Cambré, I developed a tool that uses buttons to activate macros, each of which draws one of twenty specific muqarnas units. | 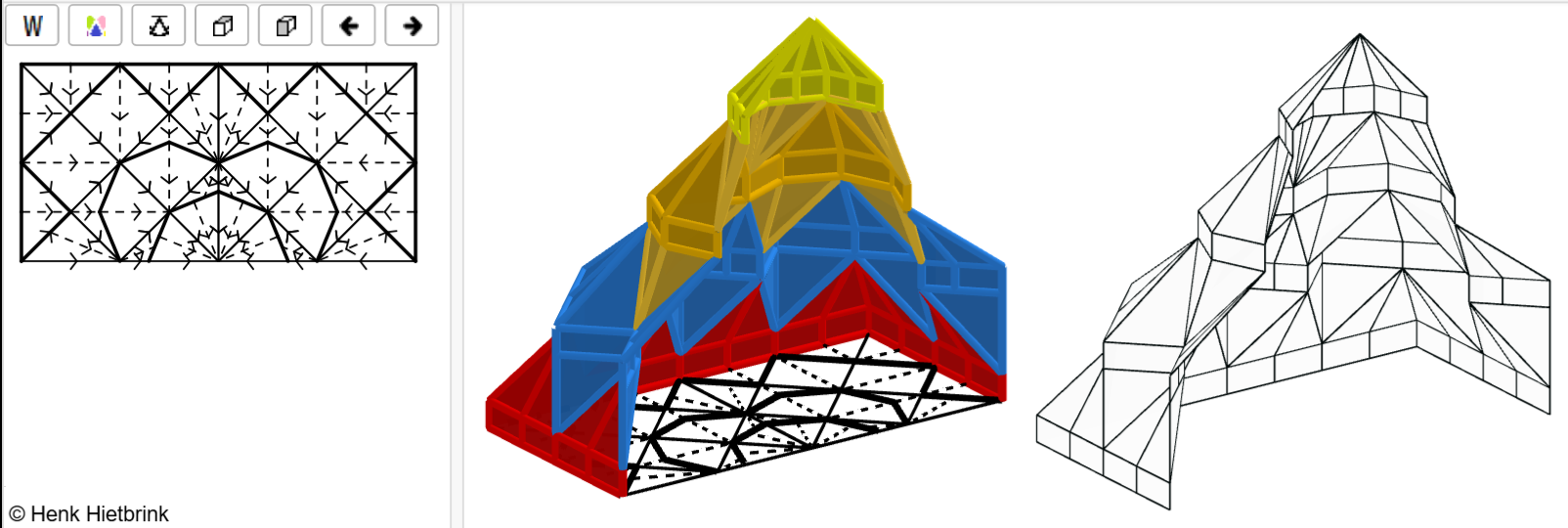 |
- Rhino Grasshopper
Rhino (or Rhino3D) is a commercial 3D computer graphics and computer-aided design (CAD) application. My Grasshopper muqarnas model has four objects, a full unit, an intermediate unit, a flat wall, and a püskül (stalactite). | 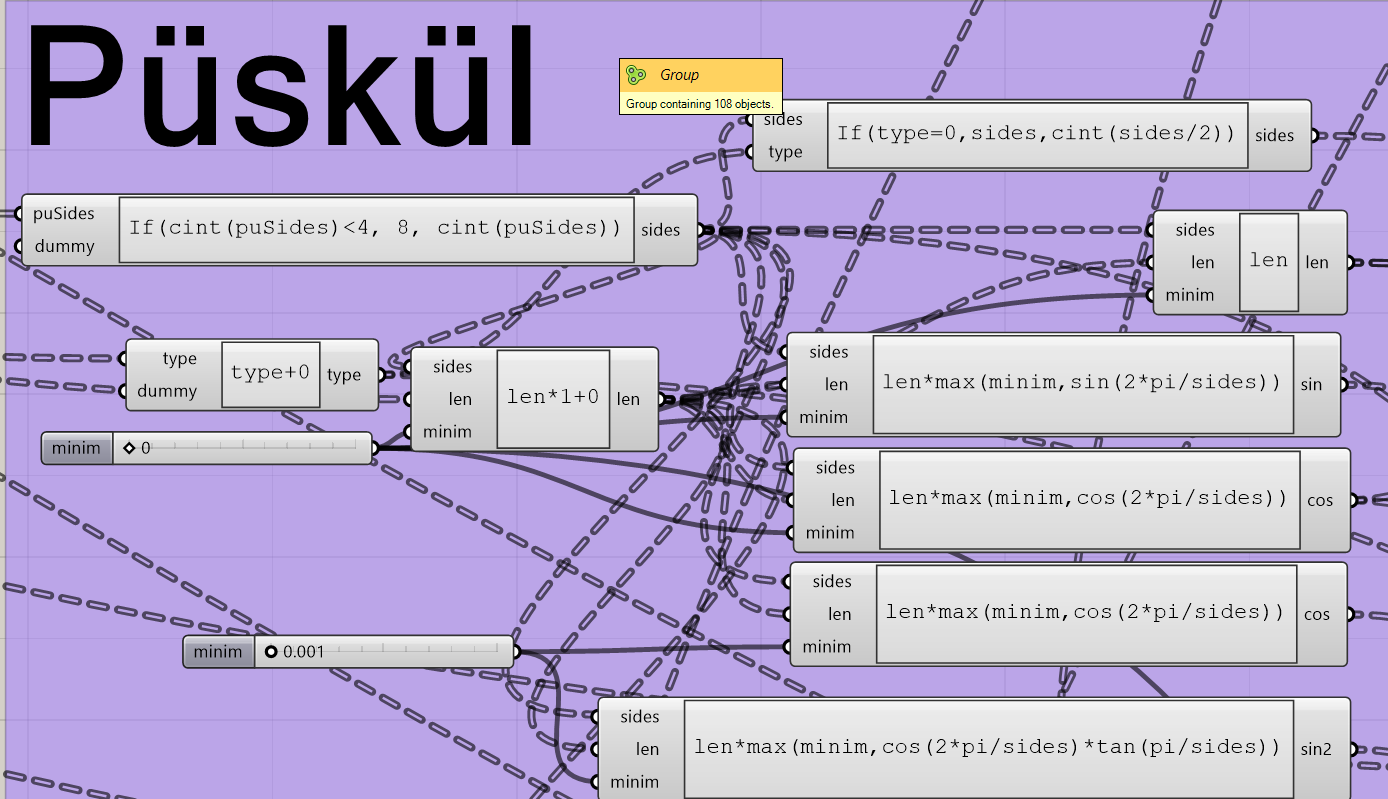 |
|
|
| 
|
Related webpages on this website:
- Aim
My research aims to develop algorithms that facilitate the transformation of 2D tessellated floor plans into 3D-printed muqarnas scale models by assigning standardized, pre-designed units. |  |
- Tiers
A definition: The muqarnas is a vaulting system based on the replication of units arranged in tiers, each of which supports another one corbeled on top of it. |  |
- Pre-designed Units
The replication of units gives rise to the idea of standardised, modular, pre-designed units. Could muqarnas units be assembled like Lego bricks? |  |
- Debate
The projection of a 3D muqarnas onto a plane forms a type of tessellation. However, a projection inherently contains less information than the original 3D structure, making it unclear whether a 2D tessellation can fully determine its 3D counterpart. |  |
- Additional Units and Exceptions
We identified many more unit types than the twelve combinations of upper and base proposed by Harmsen. |  |
- al-Kashi and his followers
For centuries, mathematicians have been intrigued by muqarnas. Their story traces back to the 15th-century Iranian mathematician and astronomer al-Kashi, who computed the area of curved surfaces. |  |
|
- Ödekan Tuncer Uluengin
Three Turkish writers on muqarnas should be mentioned: Prof. Dr. Ayla Ödekan, Prof. Dr. Orhan Cezmi Tuncer and Mehmet Fatin Uluengin. |  |
- Sakkal
Mamoun Sakkal worked on Armenian muqarnas. I explored his drawings | 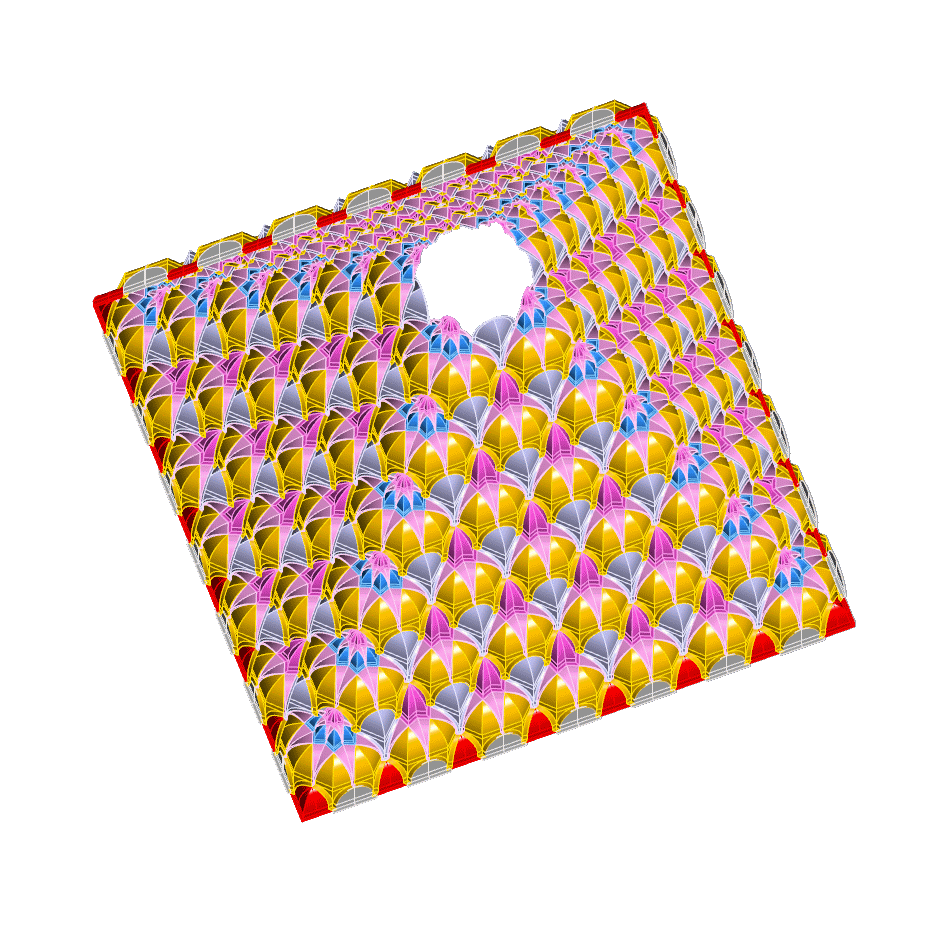 |
- Conclusions
- Literature
Over the past fifty years, leading architects and scholars in Türkiye and Iran have published significant scholarly works on muqarnas. |  |
|
- Photos
A few photos and a long list of photo repositories are available |  |
- My Instagram
Here is a list of my Instagram stories. This page is searchable and offers direct links to each Instagram story. |  |
- NWD 2025 Workshop
How much math is hidden in a muqarnas? What about symmetry and similarity? |  |
- Bridges 2025 Contribution
The figures in my contribution deserve a better stage. High resolution images are available on this webpage. |  |
- Bridges 2025 Activity
At the Family Day, participants can build a muqarnas with my Lego-like building units. |  |
|
Muqarnas as Works of Art
Have you ever stood before a mosque, gazed upward, and felt captivated by the beauty above you? You may have been admiring a muqarnas, a breathtaking work of art designed to leave you speechless. Muqarnas, found in portal hoods, beneath minaret balconies, or in the corners of prayer halls, are masterpieces of architectural ornamentation. With their variety of materials, designs, and interplay of light and shadow, these decorations have been enchanting visitors for nearly a millennium.
Photos and links to photo albums are on their own web page. My stories on Instagram include many photos.
Definition
The muqarnas is a vaulting system based on the replication of units arranged in tiers, each of which supports another one corbeled on top of it.
To truly grasp the essence of muqarnas, one must first understand its fundamental elements: units and tiers.
Depending on the material and method of construction, muqarnas can be conceived either as a standing ornament-such as a layered stacking of cut stone rising from the base,
or as a hanging ornament, such as plasterwork suspended from above by ropes attached to a frame hidden behind the muqarnas. However it is conceived, analysis of the pattern usually begins with the central star at the top.
- Tiers and Units
A definition: The muqarnas is a vaulting system based on the replication of units arranged in tiers, each of which supports another one corbeled on top of it. |  |
Mathematicians
For centuries, mathematicians have been intrigued by muqarnas. Their story traces back to the 15th-century Iranian mathematician and astronomer al-Kashi, who documented the craft of masons and their techniques for constructing muqarnas. Mathematicians dream of algorithms capable of seamlessly elevating (converting) a 2D tessellation plans into 3D muqarnas forms. It turns out that this kind of reverse engineering is as promising as it is disappointing.
- al-Kashi and his followers
For centuries, mathematicians have been intrigued by muqarnas. Their story traces back to the 15th-century Iranian mathematician and astronomer al-Kashi, who computed the area of curved surfaces. |  |
Aim
My research aims to develop algorithms that facilitate the transformation of 2D tessellated floor plans into 3D-printed muqarnas scale models by assigning standardized, pre-designed units.
I refer to this as a reverse engineering process, with the goal of integrating it into rule-based software. My tools are Rhino Grasshopper, GeoGebra, and Excel Visual Basic.
- Aim
My research aims to develop algorithms that facilitate the transformation of 2D tessellated floor plans into 3D-printed muqarnas scale models by assigning standardized, pre-designed units. |  |
Pre-designed Units
The replication of units gives rise to the idea of standardised, modular, pre-designed units. Could muqarnas units be assembled like Lego bricks?
Among others,
Harb,
Harmsen,
Sakkal,
and I had ideas.
"Pre-designed" and "pre-fabricated" are similar terms, but they're not exactly the same.
The difference matters.
In the figure above, the orange jug (top part) and the orange biped (bottom part) go together.
Almost every jug has a biped underneath, with just a few exceptions.
So, they form one pre-designed unit. But when it comes to production, only the top part (the jug) is made using a mold.
The bottom part isn't.
The same idea applies to the blue squares and red triangles. There's a mold for the top part (the pre-fabricated piece), but no mold for the bottom part.
Dold-Samplonius and Harmsen do "pre-fabricated", Sakkal does "pre-designed", Ödekan is more into "pre-designed" because of her geometric modules.
Interesting to note that the Turkish architects Uluengin, Tuncer, and Senalp pay attention to both approaches.
- Harb
Harb proposed muqarnas designs after the excavations at Takht-i Sulayman. | 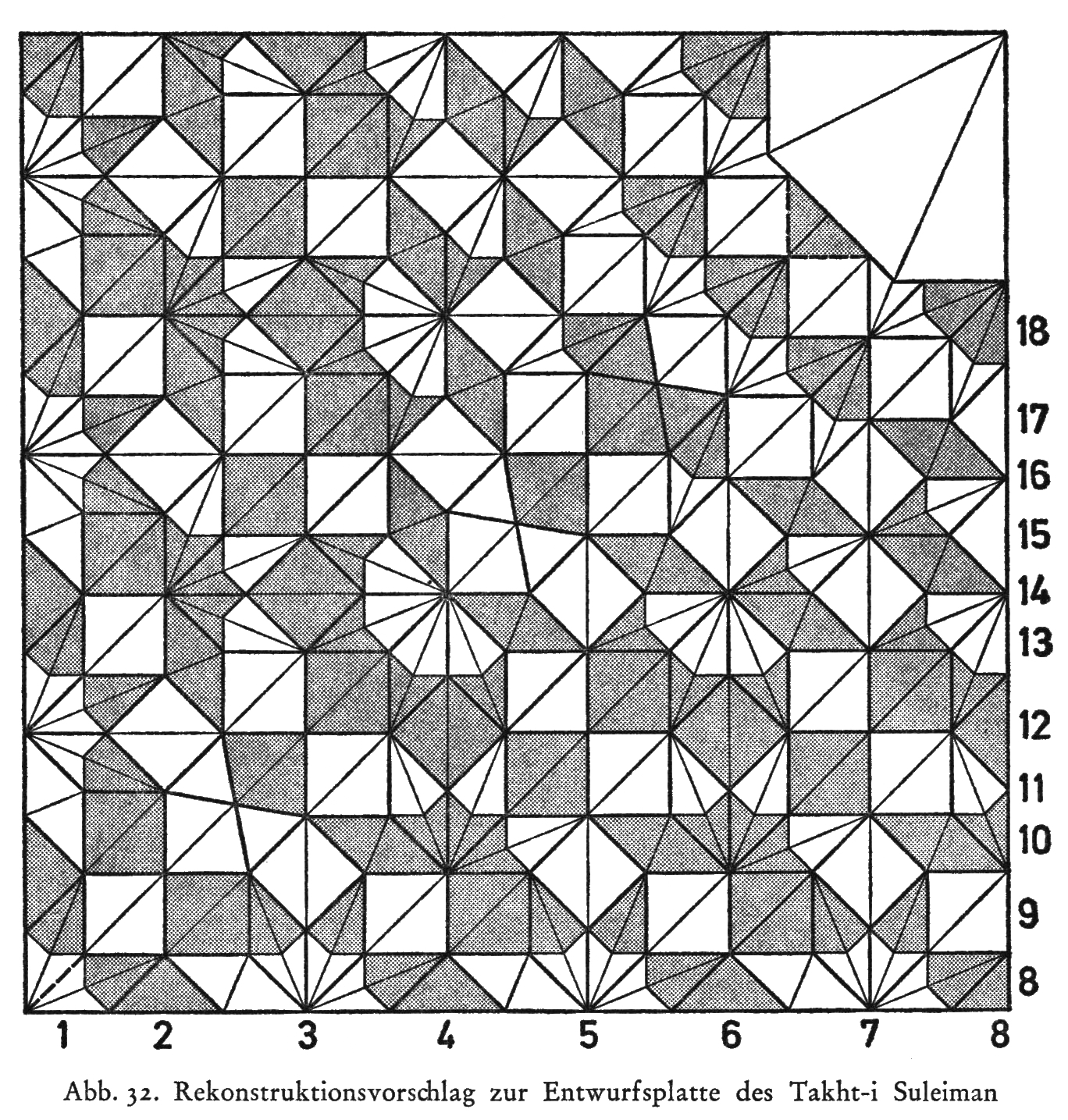 |
- Sakkal
Sakkal distinguishes more than twenty units. |  |
- Tiers and Units
A definition: The muqarnas is a vaulting system based on the replication of units arranged in tiers, each of which supports another one corbeled on top of it. |  |
- Pre-designed Units
The replication of units gives rise to the idea of standardised, modular, pre-designed units. Could muqarnas units be assembled like Lego bricks? |  |
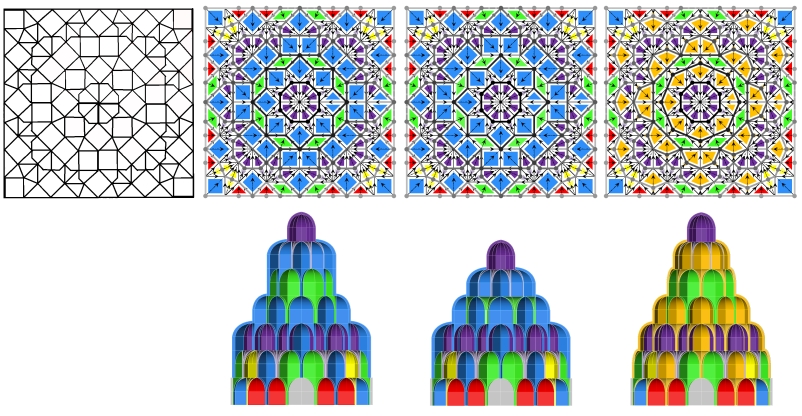
Permutations
I wrote down all permutations in the octagonal grid and counted 28 configurations.
Each unit is divided into two mirror-symmetrical triangles.
Angles are multiples of 22,5° and 8 × 22.5° = 180°.
Other configurations were rejected because they would be too large.
The next question is whether these exceptional and additional units exist in real-world examples, and the answer is yes.
Most of them can be found in Seljuk, Ottoman, and Armenian styles.
- Pre-designed Units
The replication of units gives rise to the idea of standardised, modular, pre-designed units. Could muqarnas units be assembled like Lego bricks? |  |
From 2D Floorplan to 3D printed Muqarnas: Bridging the Gap
The projection of a 3D muqarnas onto a plane forms a type of tessellation.
However, a projection inherently contains less information than the original 3D structure, making it unclear whether a 2D tessellation can fully determine its 3D counterpart.
The central challenge lies in how to "elevate" a tessellation: transforming a 2D floorplan into a 3D form by assigning pre-defined units.
- Debate
The projection of a 3D muqarnas onto a plane forms a type of tessellation. However, a projection inherently contains less information than the original 3D structure, making it unclear whether a 2D tessellation can fully determine its 3D counterpart. |  |

Rhino Grasshopper animation
© Henk Hietbrink
Excel, GeoGebra, Rhino Grasshopper, and STLviewer
Excel is my development environment to generate and analyze muqarnas floorplans.
GeoGebra is a browserbased app in the cloud. GeoGebra's ability to define and modify macros is a powerful feature. It allows users to record macros and refine them later.
Together with Chris Cambré, I developed a tool that uses buttons to activate macros, each of which draws one of twenty specific muqarnas units.
Rhino Grasshopper (or Rhino3D) is a commercial 3D computer graphics and computer-aided design (CAD) application.
My Grasshopper muqarnas model has four objects, a full unit, an intermediate unit, a flat wall, and a püskül (stalactite).
Rhino and GeoGebra can output files in many formats. STL is commonly used for interfacing with 3D printers.
ViewSTL offers an online webbased tool that shows the contents of an STL file.
This tool supports rotation, panning and zooming.
- Excel
Excel is my development environment to generate and analyze muqarnas floorplans. |  |
- GeoGebra
GeoGebra is a browserbased app in the cloud. GeoGebra's ability to define and modify macros is a powerful feature. It allows users to record macros and refine them later.
Together with Chris Cambré, I developed a tool that uses buttons to activate macros, each of which draws one of twenty specific muqarnas units. |  |
- Rhino Grasshopper
Rhino Grasshopper (or Rhino3D) is a commercial 3D computer graphics and computer-aided design (CAD) application. My Grasshopper muqarnas model has four objects, a full unit, an intermediate unit, a flat wall, and a püskül (stalactite). |  |
- STL viewer
ViewSTL offers an online webbased tool that shows the contents of an STL file. This tool supports rotation, panning and zooming. |  |
|
 planet.nl.
planet.nl.













































