A tradition of curve tracingMy favorite 17th century Dutch mathematician Frans van Schooten (1615-1660) wrote a book on mechanical devices to trace hyperbola, ellipses, and parabola. Part of this website is devoted to his book "De Organica Conicarum Sectionum ...". Each of his devices can draw only one specific conic section, for example an ellipse. The perfect compass is a much more general instrument. It can draw all conic sections. Its roots go back to 10th century Arabic sources. In Greek mathematics, one might expect perfect compasses too. Euclid mentions cutting cones at a right-angle, Apollonius mentions all kind of cones and sections, but there are no traces of a drawing device. We have to dig deeper to find physical evidence. Later on in the European Renaissance there is a revival of the perfect compass. The quest for continuous drawing curves served one goal: prove that continuous curves do exist. In the old times, mathematics was much closer to physical experiences. Curves were related to trajectories of physical objects in a controlled experiment.
|
Formulas
|
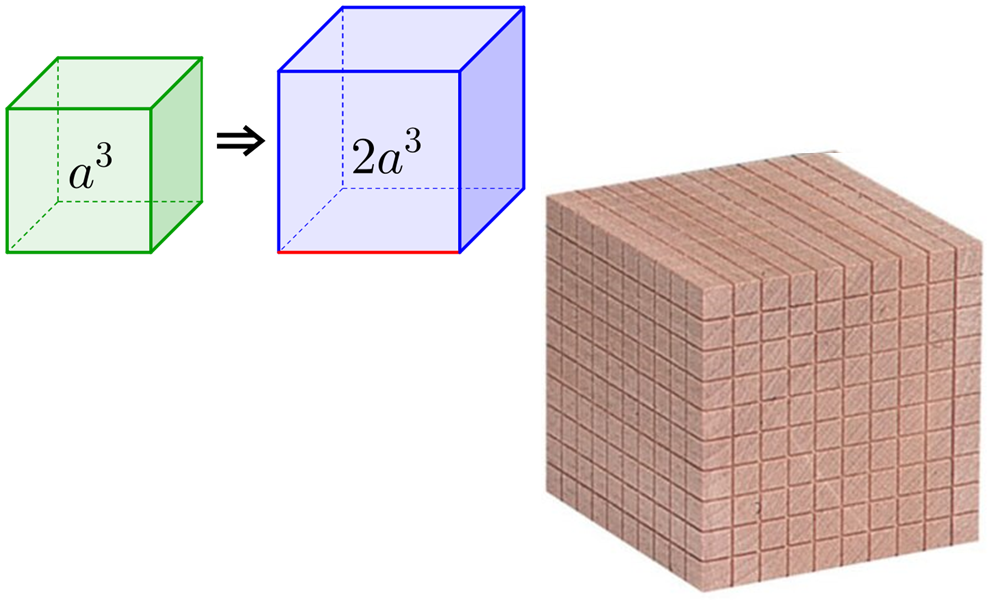
I start with an example to underline the importance of graphing parabolas. Suppose you want to double the content of a cube. Trying to solve the riddle with an integer number of small cubes does not work. You need a multiplication factor p between the base cube and the double volume cube. So p3=2 and p is not rational. | |
It is best to start with a compass that is at 45°. It produces a parabola. Suppose we want to draw the parabola 2x=y2. All we need is a perfect compass whose length is AB=√2. | |
In order to solve the problem of doubling the cube, we need a second parabola y=x2. Now we need a second perfect compass whose length is AB=½√2. To avoid having multiple perfect compasses, we could try a universal perfect compass. Of course, we can use the previous perfect compass whose length is AB=√2, but now we have to find the proper angle, which is less than 45°. For a parabola, I have a formula in which the required angle is expressed in the properties of the parabola. | |
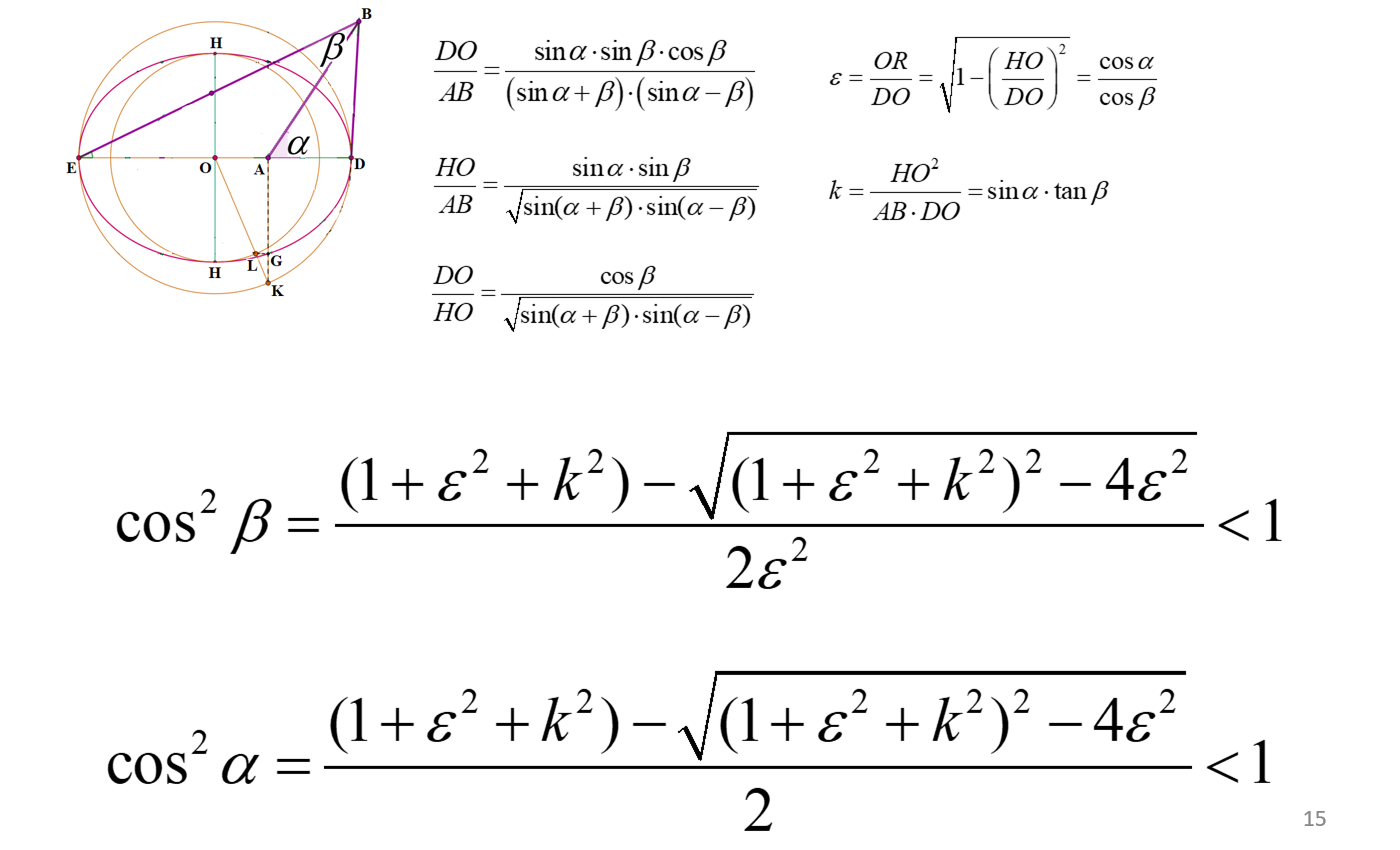
Things gets complicated for an ellipse. Given the angles, it is easy to calculate the properties of the ellipse. | |
However, the other way round, is much more difficult. Again, I have a formula. | |
If you want to draw an ellipse, the perfect compass will do, but there are many more alternatives. My favourite 17th century mathematician Frans van Schooten wrote a book on all kind of devices to produce conic sections, The gardener ellipse is so easy. |
GeoGebra
Literature
- Blåsjö, V. (2022). Operationalism: An Interpretation of the Philosophy of Ancient Greek Geometry. Found Sci 27, 587-708
 DOI
DOI
- Hogendijk, J.P. (1995). Ibn al-Haytham's Completion of the Conics. New York: Springer, Sources in the History of Mathematics and Physical Sciences no. 7
- Hogendijk, J.P. (1998). L'étude des sections coniques dans la tradition Arabe, in: Actes du 3ème colloque Maghrébin sur les Mathématiques Arabes, Tipaza. Alger: École Normale Supérieure, pp. 147-158
- Milici, P. (2020). A machine for conics and oblique trajectories
 Hal
Hal
- Raynaud, D. (2007). Le tracé continu des sections coniques à la Renaissance, in: Arabic Sciences and Philosophy , volume 17 , pp. 299 - 345, Cambridge: Cambridge University Press
 DOI
DOI
- Rashed, R. (2003). Al-Quhi et Al-Sijzi: Sur Le Compas Parfait et le Tracé Continu des Sections Coniques, in: Arabic Sciences and Philosophy, volume 13, pp. 9-43, Cambridge: Cambridge University Press
 DOI
DOI
- Rashed, R. (2005). Geometry and Dioptrics in Classical Islam, London: al-Furqan, Islamic Heritage Foundation
- Rose, P.L. (1970). Renaissance Italian methods of drawing the ellipse and related curves in: Physis, volume 12, pp 371-404, Milano: Museo Nazionale
- Sijzi, (10th century), Risala fi wasf al-Qutu al-Makhrutiyya,
 Leiden University Library
Leiden University Library
- Vittori, T. (2009). The perfect compass: conics, movement and mathematics around the 10th century in: History and epistemology in mathematics education, Proceedings of the 6th European Summer University, pp.539-548. Vienna: Verlag Holzhausen
 Hal
Hal
- Woepcke, F. (1874). Trois traités arabes sur le compas parfait, publiés et traduits par François Woepcke, in: Notices et extraits des manuscrits de la Bibliothèque impériale (Paris) 22/1874/1?175 (reprint in: F. Woepcke, Études sur les mathématiques arabo-islamiques. Nachdruck von Schriften aus den Jahren 1842-1874, Frankfurt, 1986, vol. 2, pp. 560-734 and in: Islamic Mathematics and Astronomy, vol. 66, Frankfurt 1998, pp. 33-209









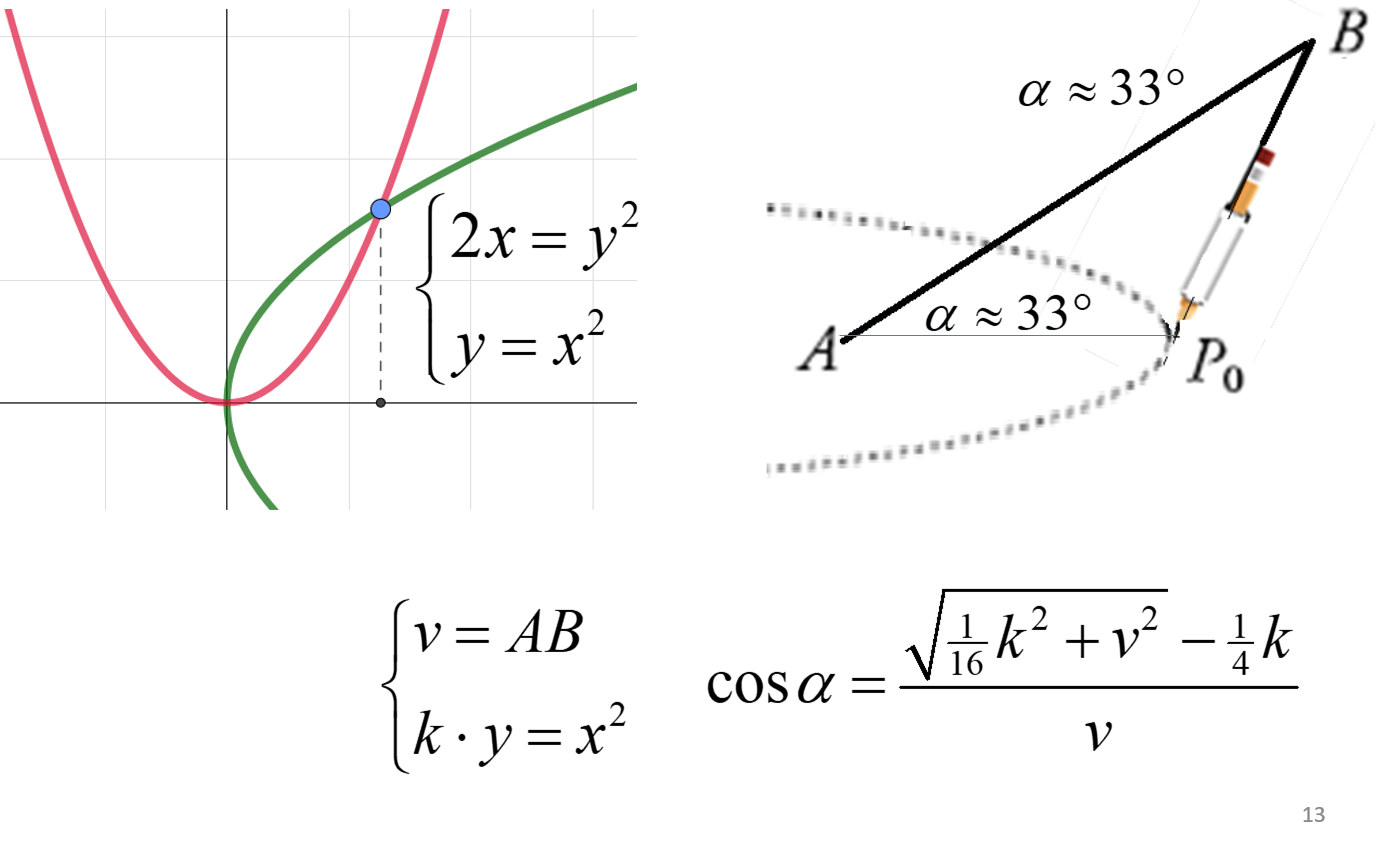


 Start animation
Start animation



