|
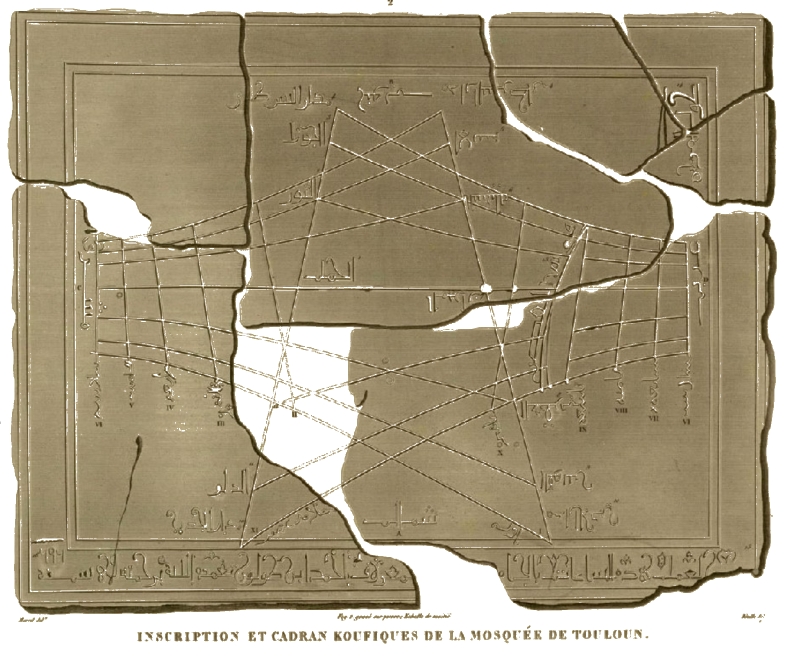
Start hereThe story of the remains of the Ibn Tulun sundial starts when mr Marcel, a member of the scientific staff of Napoleon's expeditionary force, found a broken sundial in Ibn Tulun mosque in Cairo. Unfortunately, the remains were stolen before France could steal them for a French museum. Sadly, this is the only drawing we have. The design of the sundial is quite special. We can assume that it is a horizontal sundial with north up. A curved line is visible on the left. That must be the line of the afternoon prayer asr. A replica of the sundial is on display in the Istanbul Museum. Three things stand out: The unusual interplay of lines, the double prayer line, and the relatively long gnomon are striking. | |
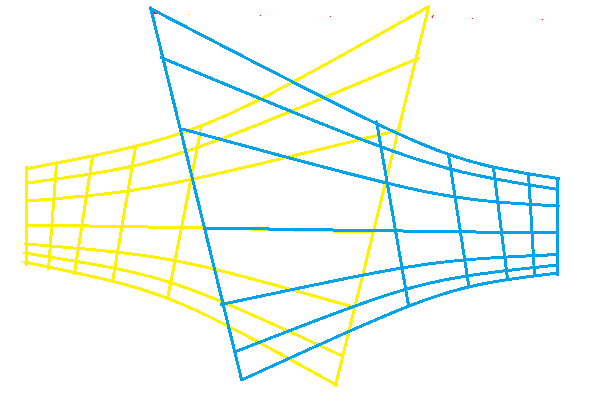
Two halvesThe line pattern doesn't resemble the usual bow tie. Louis Janin and David King already pointed out in 1978 that the sundial is unusually narrow and that the two halves should be viewed separately. The early morning hours are, as it were, superimposed over the late afternoon hours. This means the sundial has two noon lines, one on the left and one on the right. The replica should therefore have two shadow casters, each noon line with its own half and its own shadow caster. | |
Ibn al-MuhallabiIn 1425, Ibn al-Muhallabi wrote a manuscript on constructing horizontal and vertical sundials for Cairo's latitude. What is special is that the right side counts the unequal time intervals (two-thirds of an hour) after sunrise and the left side first counts the time intervals until the asr prayer and then the time intervals until sunset. | |
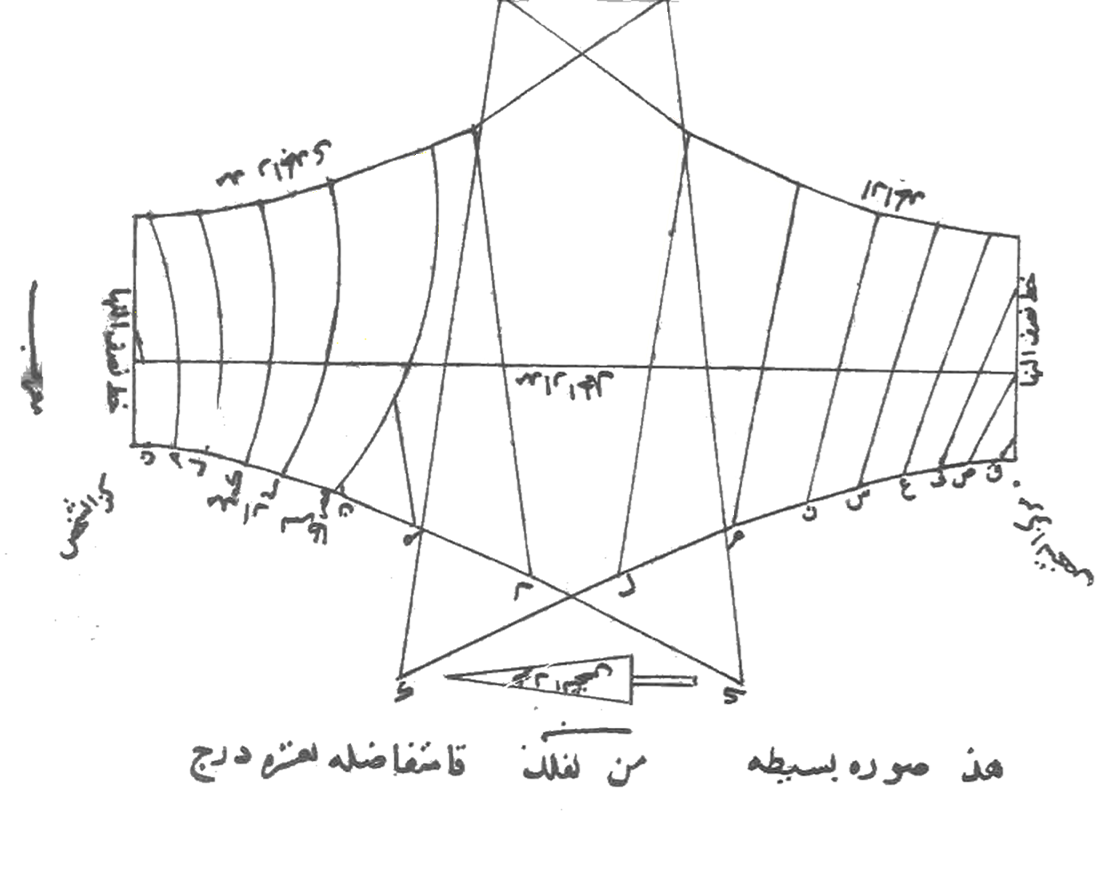
DesignBy shifting both halves, the usual image of a horizontal sundial is created. The question is whether this drawing is suitable for a sundial intended for Cairo at latitude 30°. The butterfly bow is bordered by two shadow lines. The lower one belongs to summer when the sun reaches the Tropic of Cancer, and the upper one belongs to winter when the sun reaches the Tropic of Capricorn. Between them lies a straight line. When the sun passes the equator, the shadow of the shadow caster lies on a straight line all day long. With a horizontal sundial in the northern hemisphere above 25°, all lines are north of the shadow caster and the summer line is closer to the straight line than the winter line. The conclusion is that the shadow caster should be placed at the bottom of the drawing. The length of the vertical style, the shadow caster determines the distance between the hour lines; the longer the shadow caster, the greater the spacing. Conversely, when the line pattern is given, the length of the corresponding vertical style can be calculated. With software tools, designs are made for for a horizontal sundial at 30° latitude. These designs match Marcel's drawing well. | |
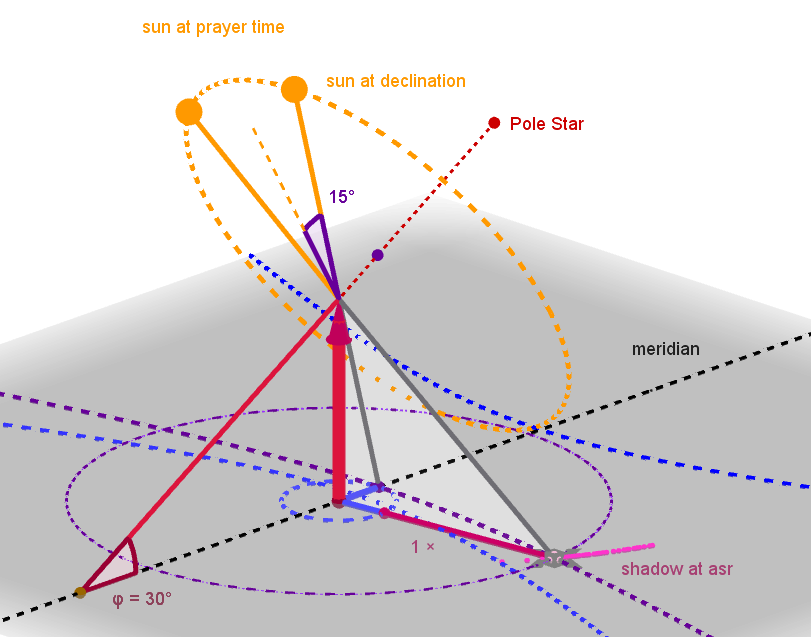
Basics of Sundial DesignTo find the correct position of the shadow caster we first need to look for some triangles and then the size of the different angles.
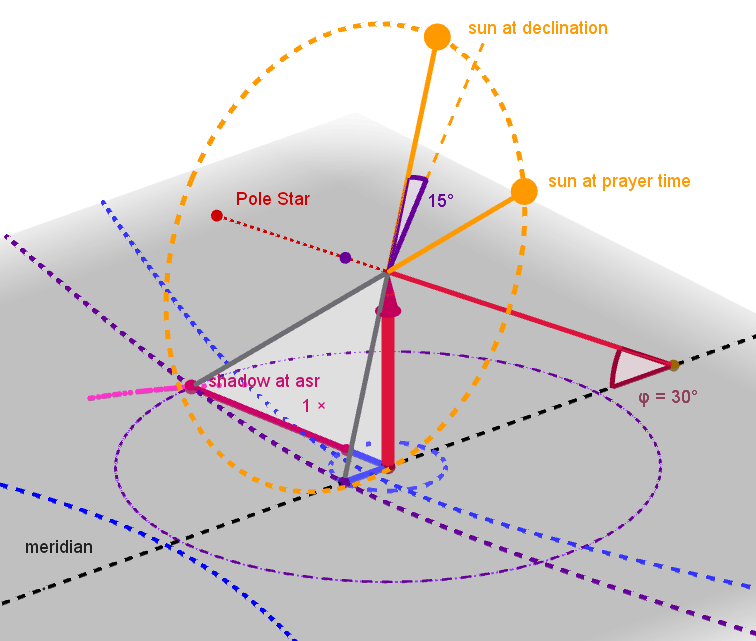
Some sundials have an oblique stick in the direction of the pole star, others a vertical stick perpendicular to the horizontal plane on which the sundial is engraved. The angle between the polar style and the horizon is exactly the latitude. That gives the first triangle. The equatorial plane is perpendicular to the polar style. On March 21st and September 23rd, the sun crosses the equator. On those days, the shadow cast by the top of the shadow caster lies on a straight line. In the second triangle (black), you can see where the shadow of the tip of the sundial falls when the sun is at its highest point at noon. With this simple drawing, we have determined the distance between the shadow caster and the shadow line. In summer, the Sun is 23° higher in the sky. The narrow third triangle indicates where the shadow falls at noon on a summer day. Similarly, in winter, the Sun is 23.4° lower in the sky. The broad fourth triangle indicates where the shadow falls at noon on a winter day. Conclusion: if you know the geographical latitude and draw the three corresponding shadow lines, the triangles are fixed. If you know the width between the sundial lines, you can calculate how long the shadow castor should be and determine exactly where it should be placed. | |
DimensionsThe relative dimensions can be calculated with basic trigonometry without knowing the exact lengths. For example, 100% is the distance between the tip of the shadow caster and the shadow position at 12:00 noon on 21 March, but also the distance between the nine o'clock line and the 12 o'clock line, as well as the distance between the 12 o'clock line and the three o'clock line. For a horizontal sundial in Cairo, the length of the vertical shadow caster is 86.6%. In the proceedings, all relevant triangles will be drawn to make the calculations even more accurate.
| |
Improving the ReplicaWith this knowledge, the replica can be improved. Two shadow casters are needed. The drawing has been measured. The relative dimensions can be converted to absolute dimensions. Measured along the meridian, the distance between the summer hyperbola and the winter hyperbola is 68.5 mm. Relatively speaking, that is 40.0% + 66.6% = 106.6% compared to the 86.6% of the relative length of the vertical style. The vertical style must then be 55.6 mm. The position relative to the equinox line is then 32.1 mm. | |
Prayer time AsrFor this sundial, the Asr prayer time is defined this way: the time at which the shadow of a stick is equal to the length of the shadow of that stick at noon, plus once the length of the stick. There are several ways to determine the correct time. A simple method for determining the prayer time is to draw a line at noon near the shadow at noon and then draw an arc with a radius longer than one time the length of the stick. And then wait until the shadow reaches the arc. With this daily routine, you can find the prayer time for noon without a sundial. The triangle with the two circles indicates how high the sun is in the sky for afternoon prayer on that particular day with that particular declination. Step one was to draw those circles. Step two is to calculate what time corresponds to that sun height. Or what sun direction corresponds to that sun height. In the drawing, this was done geometrically. The algebraic approach with essential formulas will be included in the proceedings. In the second drawing, the viewpoint has been rotated to make the triangle stand out better. | |
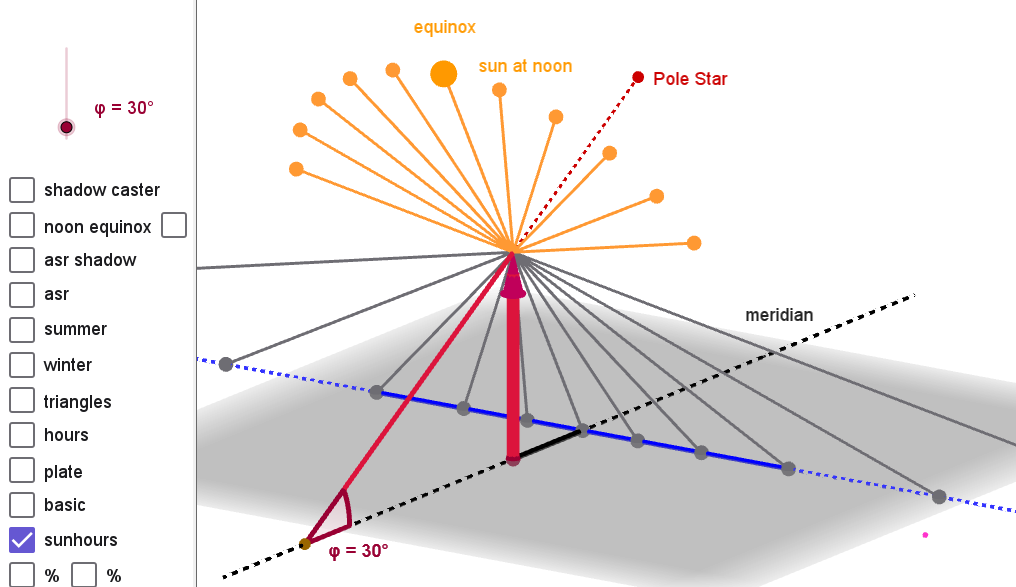
GeoGebra Animation
Below is an image of the animation with Geogebra. Click on the image and the animation starts. The animation includes a stepwise explanation how all lines, circles and curves can be drawn, including the Asr prayer line. The animation can be configured for every latitude.
Sources
Here are links to libraries.
- Chester Beatty Library: All Microfilms
- Gallica: Description de l'Egypte ou Recueil des observations et des recherches qui ont été faites en Egypte pendant l'expédition de l'armée française
- Napoleon.org: Description de l'Egypte
- Bibliotheca Alexandria: Description de l'Egypte
- David King: Islamic Sundials
- Istanbul Museum of Science and Technology in Islam: Collection of Objects
- Istanbul Museum of Science and Technology in Islam: Overview of Animations
Literature
- Chester Beatty Library: CBL_Ar_3641 a treatise on gnomonics by the Egyptian muwaqqit Ibn al-Muhallabi, written in Cairo in 829 H. 1425-26 AD
- D. King, L. Janin, 1978 - Le cadran solaire de la Mosquée d'Ibn Tulun au Caire
- J.J. Sédillot: Traité des instruments astronomiques des arabes, composé au treizième siècle par Aboul Hhassan Ali, de Maroc, intitulé Jami' al-mabadi' wa-al-ghaat (collection des commencements et des fins) Traduit de l'arabe sur le manuscrit 1147 de la Bibliothèque royale
- Sezgin Islamic Architecture Reprints volume 14: J.J. Marcel: Mémoire sur la mosquée de Touloun et les inscriptions .1830
- Sezgin Islamic Architecture Reprints volume 14: E.K. Corbet: The Life and Works of Ahmad ibn Tûlûn. (1891)
- G. Ferrari, Le Meridiane dell'Antico Islam, Il tempo nella civiltà islamica Caratteristiche, descrizione e calcolo dei quadranti e degli orologi solari islamici
Websites
- Staatsbibliothek Zu Berlin: Marrakushi Sharaf al-Din Abu Ali al-Hasan ibn Ali ibn Umar al-Marrakushi
- ArchNet: Jami ibn Tulun Cairo, Egypt












 Start animation
Start animation