Servants Of MathesisThis webpage provides all links, references, figures and tables mentioned in our article "Servants of Mathesis": Early modern education in fortification and the authority of mathematics in the Dutch language, by Charles van den Heuvel and Henk Hietbrink.
|
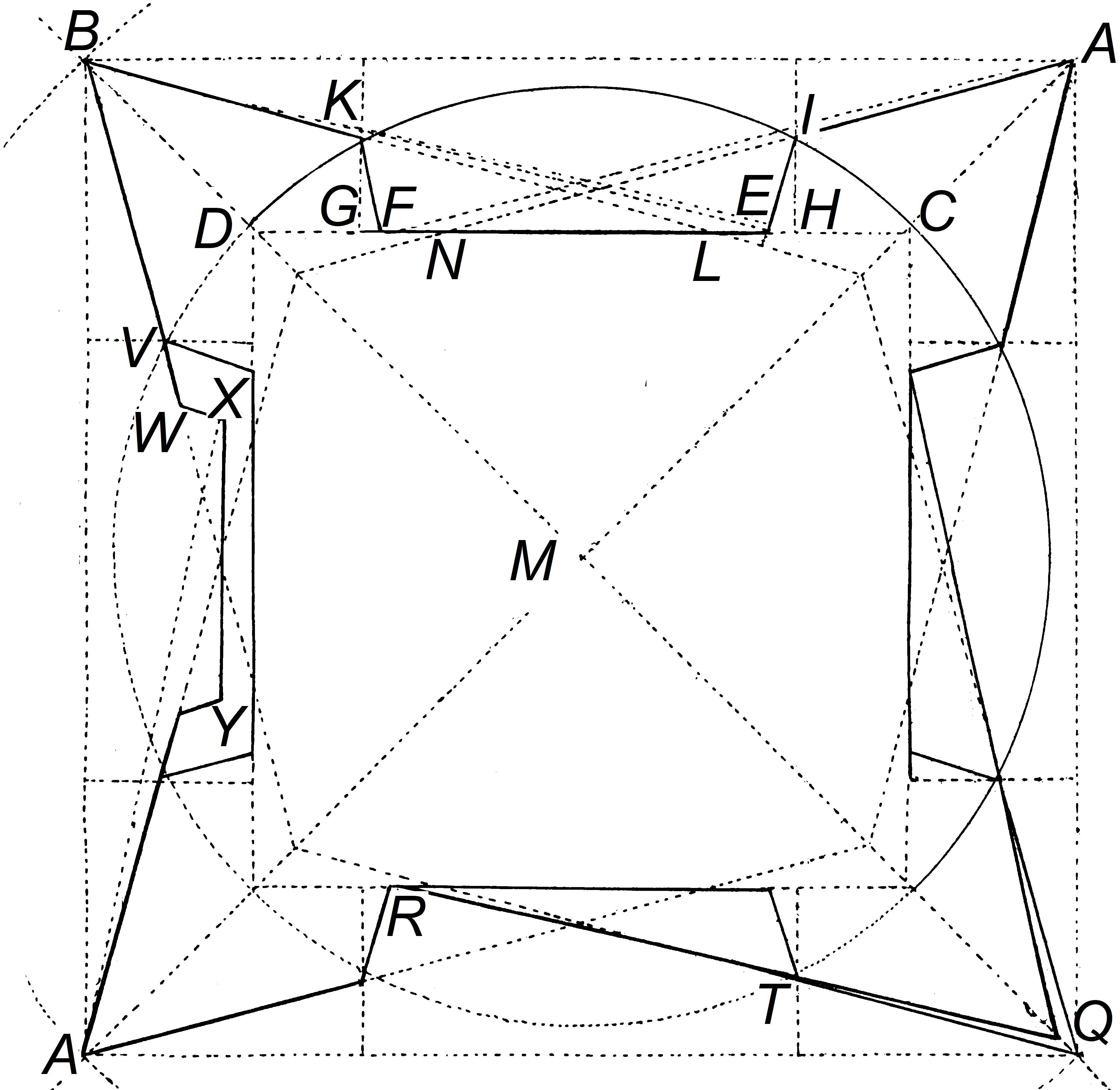
Figure 1: Transition of cross-section line drawing of bastion and curtain into more detailed profile
We are well informed about the teaching materials of the Van Schooten family. Leiden University holds several manuscripts. First, there is the autograph of Frans van Schooten Sr. mentioning explicitly his name in the part on fortification with the title Mathematische Wercken door F. van Schooten in multiple parts dealing with geometry, surveying and fortification. Another anonymous manuscript (here called the Lombaerde manuscript after the private owner who reconstructed the order of it). It has a very similar layout of pages, although the handwriting of the Leiden manuscript is in cursive unlike the Leiden copy and therefore it is hard to establish whether the two indeed could be written by the same hand. The Leiden manuscript has been colored in beautifully with much attention to presentation not only in its appearance but also in its contents. It contains for instance many examples how to translate step by step two-dimensional line drawings into three dimensional ones and details such as complete scale rods.
Sources: Frans van Schooten Sr. BPL 1013 [fol. 219 v. and fol. 220 v.] (right)
Persistent URL to BPL 1013 fol. 219 v.
Persistent URL to BPL 1013 fol. 220 v.
BPL 1013
Full color illustrations are available at Leiden University Libraries Digital Collections.Persistent URL to Leiden University Libraries Digital Collections
The rights status of this resource is public domain
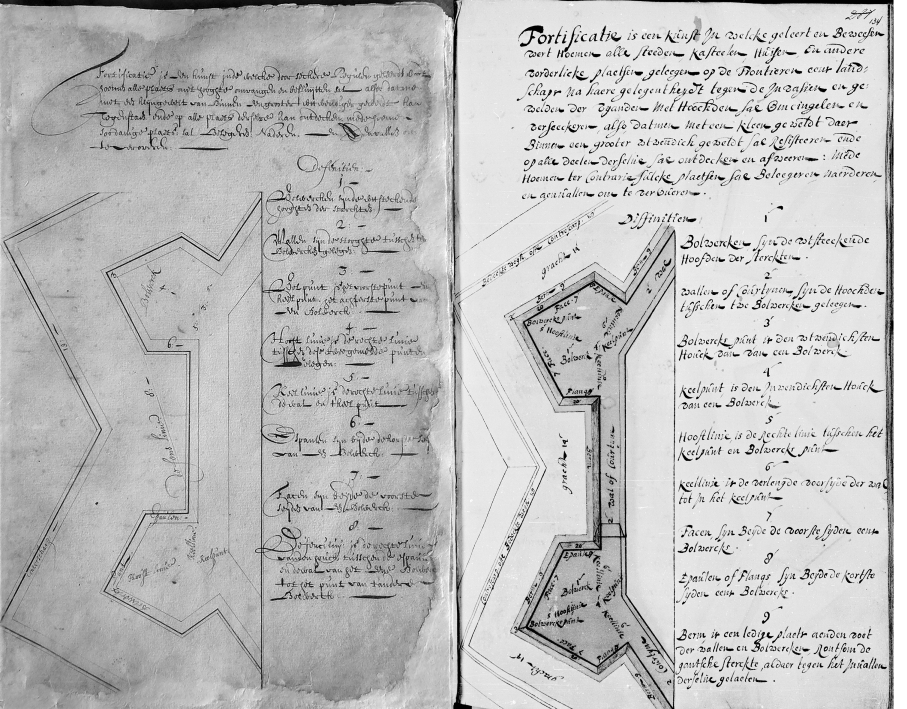
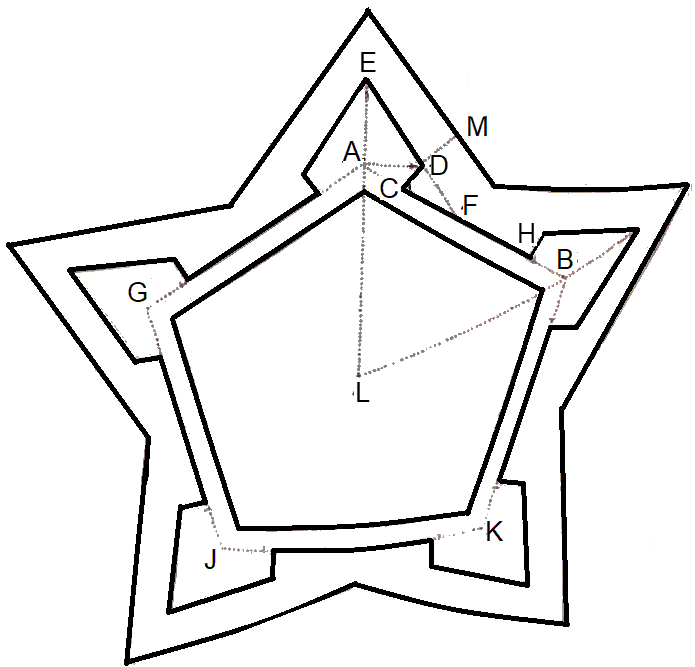
Figure 2: Two bastions and curtain with definitions
Following the academic custom of the time, Frans van Schooten Sr. opens his manuscript with definitions and propositions.
Sources: Lombaerde manuscript [fol. 1 r.] (left): and Frans van Schooten Sr. BPL 1013 [fol. 134 r.] (right).
Persistent URL to BPL 1013 [fol. 134 r.]
BPL 10133
Full color illustrations are available at Leiden University Libraries Digital Collections.Persistent URL to Leiden University Libraries Digital Collections
The rights status of this resource is public domain
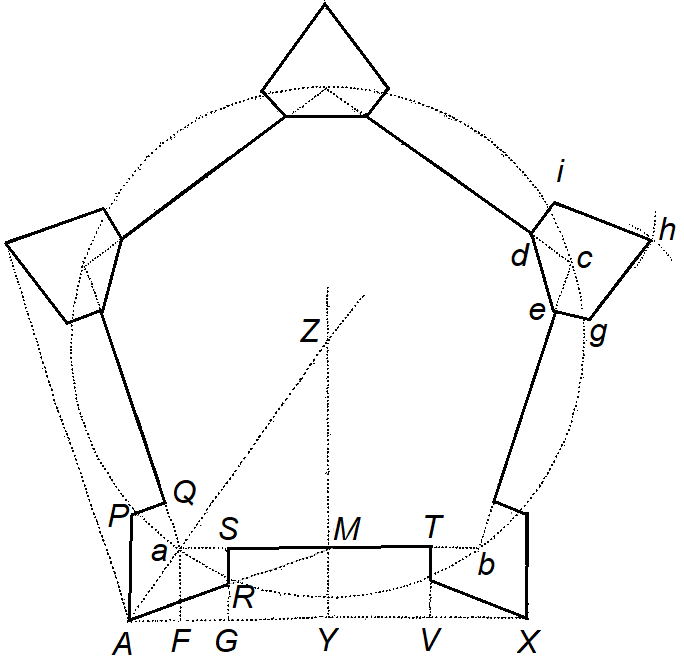
Figure X: Design pentagonal fortress with corner and curtain bastions
Simon Stevin favored the regular hexagonal citadel, but his successors showed concepts with pentagonal or hexagonal plans as ideal, although in practice terrain conditions called for other, less regular layouts. In HS 441, Pieter van Schooten described a pentagonal Small Royal with a bastion angle which is 30° more than one-thirds of the polygon angle. He describes a typical Small Royal fortification with a 60 rod distance between the points of the two bastions.
a mathematical analysis of Petrus van Schooten pentagonal fortress
Sources: Petrus van Schooten Groningen University Library, HS 441 [fol 173.] and Christiaan Huygens, Leiden University Library, Hug 16 [fol. 31 r.].
Persistent URL to HS 441 [fol 173.]
Persistent URL to HUG 16 [fol 31 r.]
On request of the publisher, this drawing was removed from the article. Four illustrations was the maximum allowed.
HS 441
Full color illustrations are available at University of Groningen Library, Special Collections.Persistent URL to University of Groningen Library, Special Collections
Copyright UBG. Free use for non-commercial purposes. In publications, "University of Groningen Library, Special Collections" must be mentioned as source.
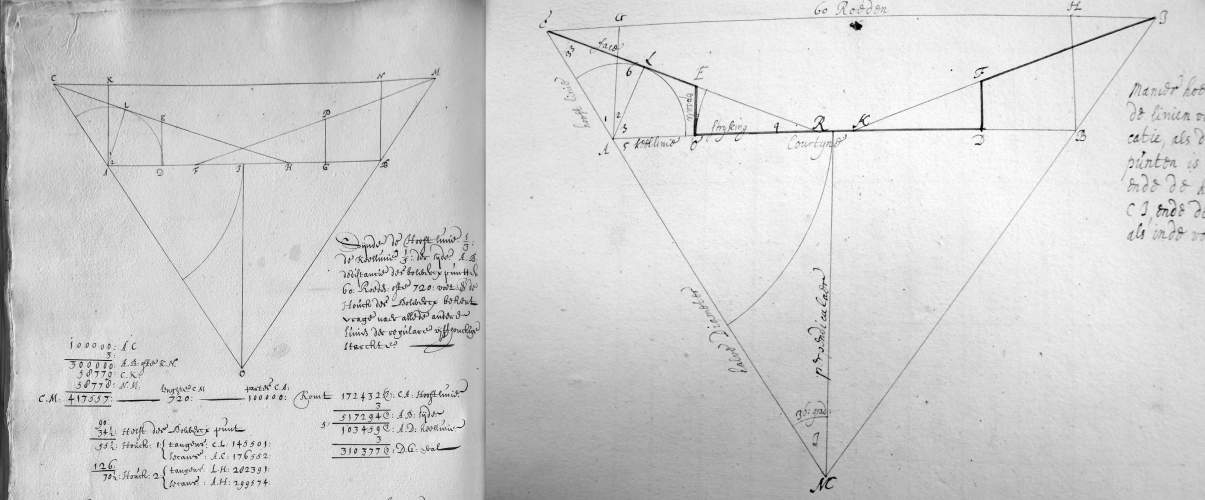
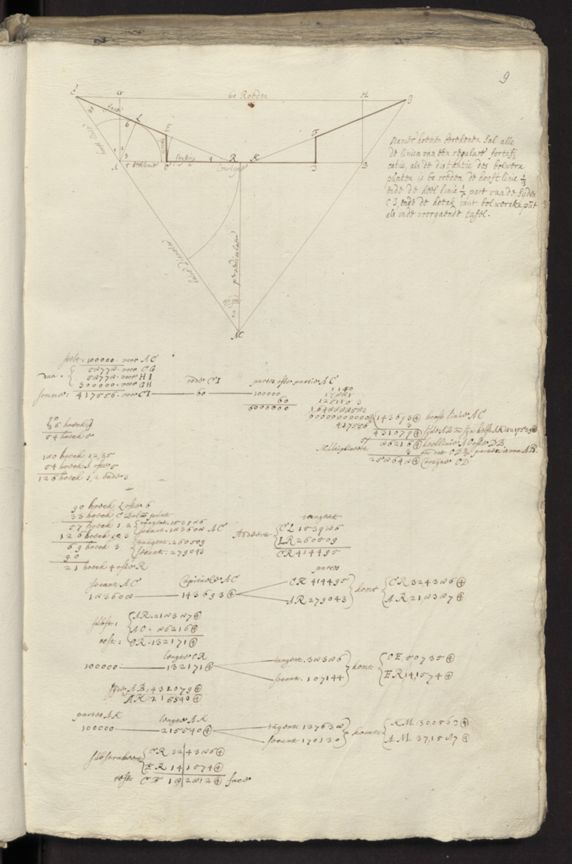
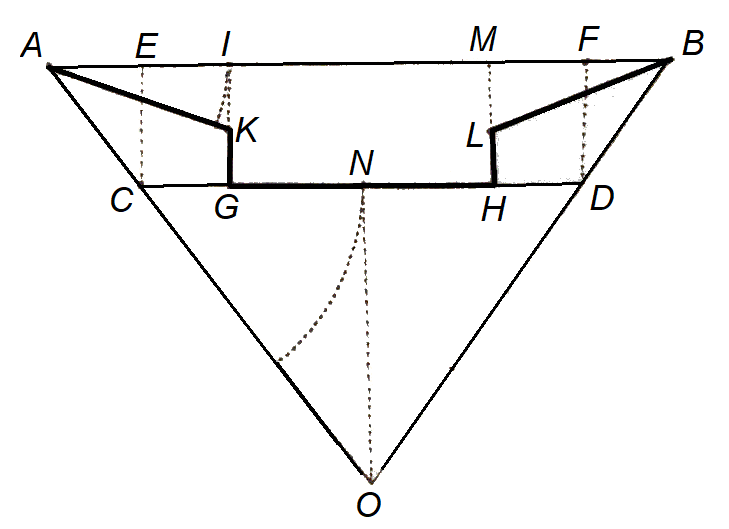
Figure 3: Design two bastions and curtain with complex goniometric rules
Surprisingly enough the layout of the more complex irregular fortifications followed basic rules while the explanation of the most elementary parts of fortification, the design of two bastions with the intermediate curtain or the construction of regular fortresses, sometimes included alternative, more complex mathematical rules. They included cosines, tangent, and secant rules and trigonometrical tables. A less surprising observation is that mathematicians rather than engineers with merely fortification expertise were using these more complex explanations or trigonometrical tables to demonstrate that the time-consuming step-by-step geometrical constructions could be replaced by alternative goniometric rules.
a mathematical analysis of Petrus van Schooten
Sources are Lombaerde manuscript [fol. 10 v.] and Petrus van Schooten BPL 1993 [fol. 9 r.].
Persistent URL to BPL 1993 [fol. 9 r.].
BPL 1993
Full color illustrations are available at Leiden University Libraries Digital Collections.
Persistent URL to Leiden University Libraries Digital Collections
The rights status of this resource is public domain.
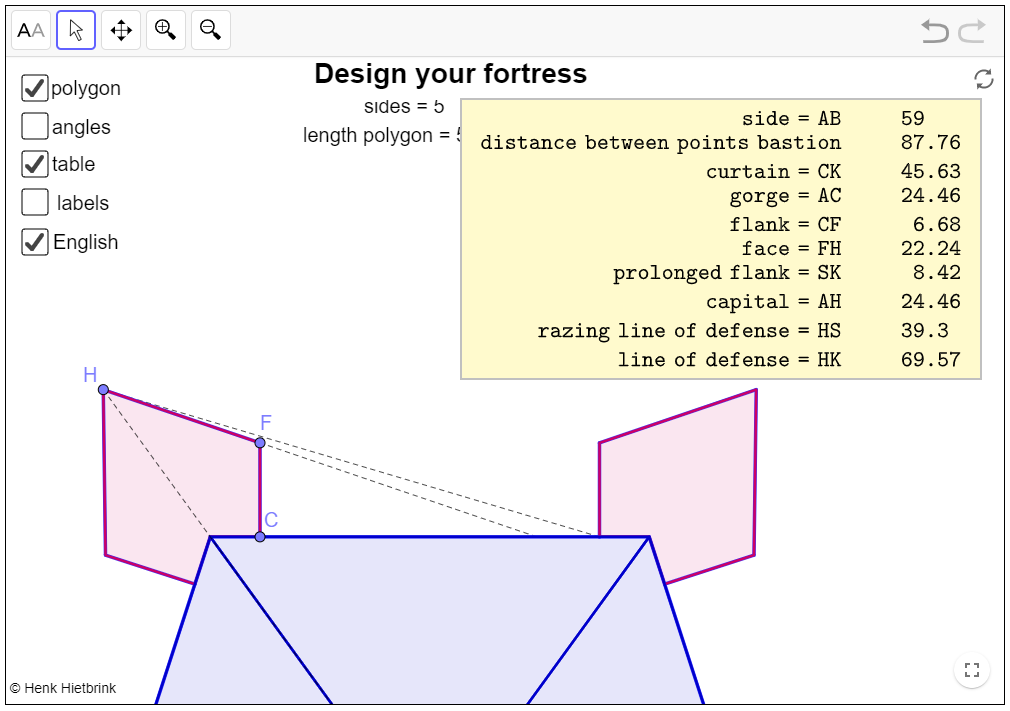
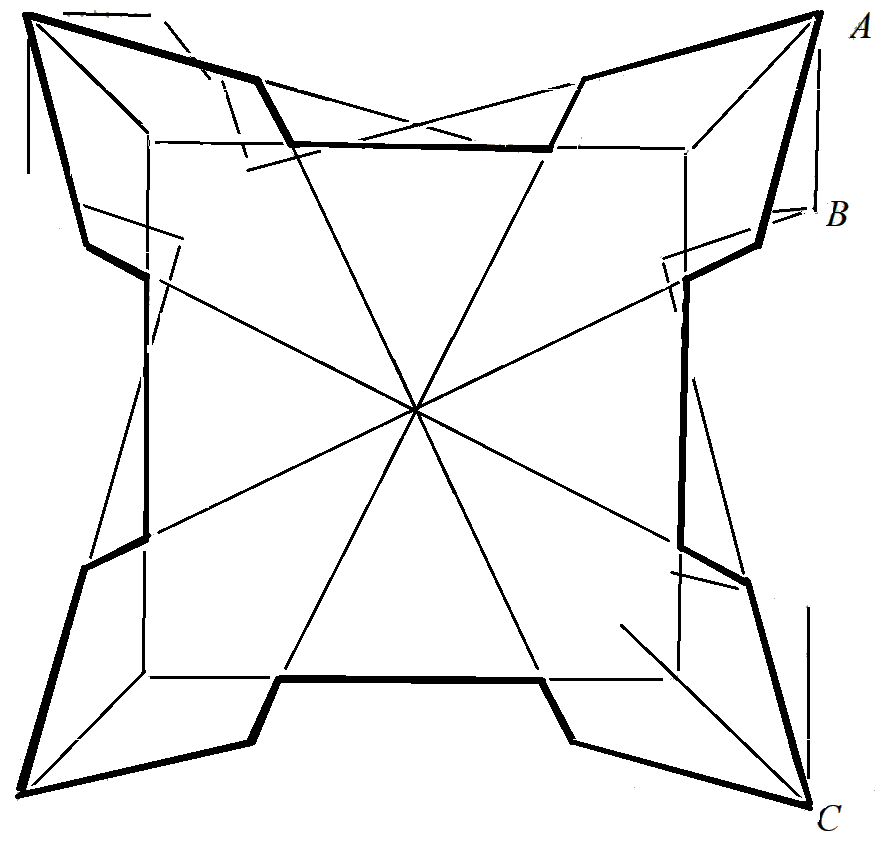
Figure 4: GeoGebra overlay of two fortification systems
Henk Hietbrink set up a rich website to encourage pupils to build their own fortresses, to analyse in the e-book Fortification in the sixteenth and seventeenth century,
included in the digital educational system GeoGebra, the geometrical constructions and calculations of fortifications in handwritten and printed treatises on military architecture
and to compare these historical examples by overlaying their designs.
For the Dutch Society of Teachers of Mathematics, (NVvW in Dutch) he wrote a lesson series on fortification trigonometry.
These examples are not only interesting to make mathematics less abstract for pupils but gives them as well insight in some of the most important historical features of the early modern city, fortifications with bastions.
- GeoGebra Book: Fortification in the Netherlands in the 17th century
- NVvW workshop "Vestingbouw als context voor sinus-, cosinus- en tangensregel"
GeoGebra
You can draw a fortress of your own to investigate the relationships between sides and angles.
You can use this animation to compare fortifications schemes of eminent engineers.
You can use this animation to compare more than 200 drawings of fortifications.
GeoGebra Book: Fortification in the Netherlands in the 17th century
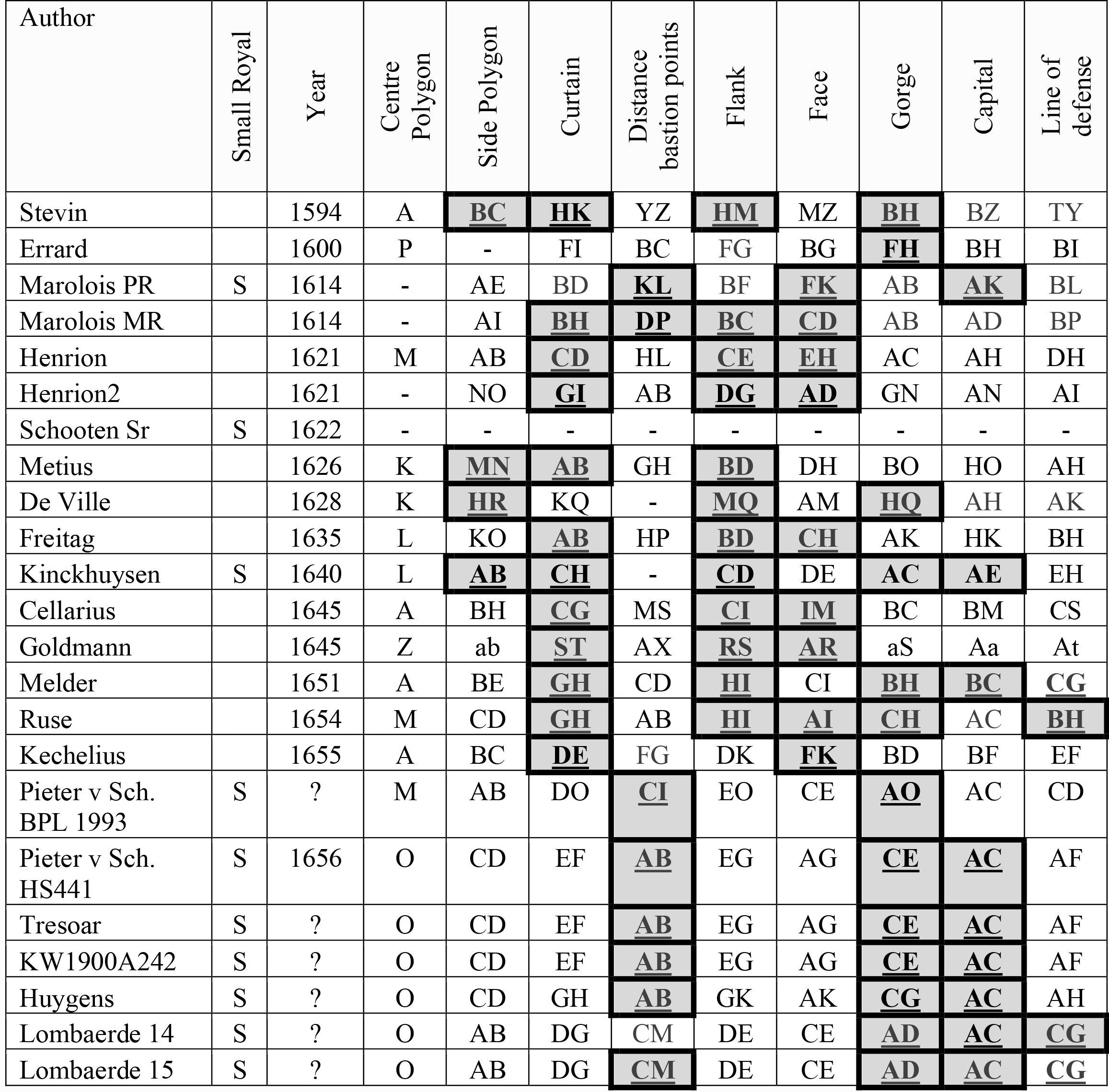
Table 1: Comparative analysis manuscripts/publications on fortification
To test our hypotheses the following questions were formulated: Can we detect some order in the design methods for the layout of fortifications and do these changes over time in correspondence with former statements of various styles in fortification? Can we detect some order in the mathematical construction and calculations of the geometrical figures underlying the design of fortifications proposed in the manuscripts and printed works, and changes herein? How complex are these design methods, are they more complex than required for the layout of fortification, and does the complexity increase over time? Although far more research needs to be done, we came to the following observations based on this preliminary comparative analysis.
Detailed description of all the fortifications mentioned in the table.
Manuscripts/Primary Sources
This list links to a webpage with more details and references to online libraries
- Anonymous, KB National Library of the Netherlands, KW1900A242
In this pentagonal design, the distance between the points of the two bastions is 60 rods (226 meters). The bastion angle is 30° more than one-thirds of the polygon angle. The length of the line of defense is 45 rods (170 meters). This is typically a Small Royal fortification

Anonymus (Koninklijke Bibliotheek): KW1900A242 date unknown
- Anonymous, Leeuwarden Tresoar, Ms 668
In this pentagonal design, the distance between the points of the two bastions is 60 rods (226 meters). The bastion angle is 30° more than one-thirds of the polygon angle. The length of the line of defense is 45 rods (170 meters). This is typically a Small Royal design.

Anonymus (Tresoar): anonymus date unknown
- Joos Crommeling and Samuel Kechelius, Beginsel der Geometrie, Leiden University Library, BPL 1351
In the pentagonal design of Kechelius, the distance between the points of the two bastions is around 81 rods (306 meters). The bastion angle is 15° more than half of the polygon angle. The length of the line of defense is 61 rods (230 meters). So, this is a Great Royal design.

Samuel Kechelius: BPL 1351 1655
- Adriaen van Cuijck van Meteren, Fortificatie [.], Leiden, University Library, BPL 3457
In this pentagonal design, the distance between the points of the two bastions of a hexagon is 60 rods (226 meters). The bastion angle is 30° more than one-thirds of the polygon angle. The length of the line of defense is 45 rods (170 meters). So, this is a Small Royal design.

Adriaan Cuijck van Meteren: BPL 3457 date unknown
- Hugo Grotius 'Mathematica Principis Mauritii' in Poemata Collecta & magnam partem nunc primum edita à fratre Guilielmo Grotio, Leiden: A. Clouquium, 1617 II, 62-71.
- Hugo Grotius, Batavi, Parallelon rerumpublicarum liber tertius etc., ed. Johan Meerman Haarlem: Adriaan Loosjes Pz, 1801-1803.
- Christiaan Huygens, Frans van Schooten Jr. Algebraicae variorum [..] cum Chr. Hugeni, annotationibus Leiden University Library, Hug 12.
- hristiaan Huygens, Van stercktenbouwen, Leiden University Library, Hug 16
In this pentagonal design, the distance between the points of the two bastions is 60 rods (226 meters). The bastion angle is 30° more than one-thirds of the polygon angle. The length of the line of defense is 45 rods (170 meters). This is typically a Small Royal design.
Christiaan Huygens: HUG 16 ±1650
- Gerard Kinkhuysen, Leiden University Library, BPL 3766
In the pentagonal design of Kinckhuysen, the distance between the points of the two bastions is 62 rods (234 meters). The bastion angle is is 30° more than one-thirds of the polygon angle. The length of the line of defense is 46 rods (173 meters). So, this is a Small Royal design.
Gerard Kinckhuysen: De Theorie der Fortificatie ofte Sterck Bovwinge 1640
- Jean Nicholas de Parival, Vermaecklijkheden van Hollandt [..]. Amsterdam: Samuel Imbechts, 1660-61.
- Hendrik Ruse, The Strengthening of Strong-Holds: invented on several occasions, and practised during the late wars, as well in the United Provinces, as in France, Germany, Italy, Dalmatia, Albania, and the neighbouring countries. London, In the Savoy: Printed by the assigns of John Bill and Christopher Barker, 1668.
The distance between the points of the two bastions is around 80 rods (300 meters). The bastion angle is about 15° more than half of the polygon angle. The length of the line of defense is 59 rods (222 meters). So, this is a Great Royal.
Henrik Ruse: Versterckte Vesting 1654
- Hendrik Ruse, The Strengthening of Strong-Holds: invented on several occasions, and practised during the late wars, as well in the United Provinces, as in France, Germany, Italy, Dalmatia, Albania, and the neighbouring countries. London, In the Savoy: Printed by the assigns of John Bill and Christopher Barker, 1668.
- Frans van Schooten Sr., Leiden University Library, BPL 1013.
In BPL 1013, Frans van Schooten Sr did not mention computational results. He assumes that the distance between the points of the two bastions is 60 rods (226 meters). The bastion angle is 15° more than half of the polygon angle. So, the design is a Small Royal.
Frans van Schooten Sr: BPL 1013 1622
- Frans van Schooten Sr., [circle of?] Lombaerde manuscript [private collection].
In this pentagonal design, tThe distance between the points of the two bastions is 81 rods (306 meters). The bastion angle is 15° more than half of the polygon angle. The length of the line of defense is 60 rods (226 meters). This is typically a Great Royal design.

Anonymus (Lombaerde): date unknown
- Petrus van Schooten, Versterkingskunst, Leiden University Library, BPL 1993.
In this pentagonal design, the distance between the points of the two bastions is 60 rods (226 meters). The bastion angle is 15° more than half of the polygon angle. The length of the line of defense is 45 rods (170 meters). This is typically a Small Royal design.

Pieter van Schooten: BPL 1993date unknown
- Petrus van Schooten, Groningen University Library, HS 441.
In this pentagonal design, the distance between the points of the two bastions is 60 rods (226 meters). The bastion angle is 30° more than one-thirds of the polygon angle. The length of the line of defense is 45 rods (170 meters). This is typically a Small Royal design.

Pieter van Schooten: HS 441 1656
- Johan Sems and Jan Pietersz. Dou, Pracktijk des Landmetens. Amsterdam: Willem Jansz., 1600.
- Simon Stevin, De Sterctenbouwing, Leiden: Frans van Ravelingen (1594) in: Principal Works of Simon Stevin, Vol. IV, ed. W.H. Schukking, Amsterdam: C.V. Swets & Zeitlinger, 1964.
In Stevin's hexagonal design, the distance between the points of the two bastions is 1237 feet (about 100 rods or 3800 meters). The bastion angle is obtuse. The length of the line of defense is 968 feet (about 81 rods or 300 meters). This design is larger than a Great Royal.

Simon Stevin: Sterctenbovwing 1594
- Simon Stevin, Maniere ende Ordre die sijn Excie verstaen heeft sal worden achtervolght int doen van de Nederduytsche lessen in the universiteyt tot Ley¬den tot onderrichtinghe ende bevorderinghe der ghene die hun ten dienste van den lande sullen begheven tot oeffeninghe van het ingenieurschap ende andere mathematische consten. (Leiden: Jan Paedts Jacobsz. 1600. Printed version: Dutch National Maritime Museum in Amsterdam Bibliotheek B-I-0073 (II,37) and manuscript Gemeentearchief Bibliotheek Leiden LB 36949 portefeuille.
Transcription of Simon Stevin's instruction for the Duytsche Mathematique.

- Simon Stevin, Wisconstighe Ghedachtenissen, inhoudende t'ghene daer hem in gheoeffent heeft den Doorluchtichsten Hooghgheboren Vorst ende Heeren, Maurits, Prince van Oraengien. Leiden: Jan Bouwensz.,1605-1608.
Literature
- Aa, A.J. van der Biografisch woordenboek der Nederlanden. Deel 10, Haarlem: J.J. van Brederode, 1862.
- Dold-Samplonius, Yvonne "Die Handschriften der Amsterdamer Mathematischen Gesellschaft" Janus, revue international de l'histoire des sciences, de la medicine, de la pharmacie et de la technique, 55, (1968): 241-303.
- Dopper, Jantien. A life of learning in Leiden. The mathematician Frans van Schooten (1615-1660), PhD thesis Utrecht, 2014.
On Feb. 12, 2014, Jantien Dopper received her doctorate from the Faculty of Science in Utrecht for her research on Frans van Schooten.

- Fara, Amelio. La città da Guerra. Turin: Einaudi Editori, 1993.
- Hale, John Rigby, "The Early Development of the Bastion: An Italian Chronology," in John Rigby Hale (ed.) Renaissance War Studies. London: Bloomsbury Academic, 1983.
- Heuvel, Charles van den. 'Papiere Bolwercken': De introductie van de Italiaanse stede
- en vestingbouw in de Nederlanden (1540-1609) en het gebruik van tekeningen. Alphen aan den Rijn: Canaletto, 1991.
- Heuvel, Charles van den, "Le traité incomplet de l'Art Militaire et l'ínstruction pour une école des ingénieurs de Simon Stevin." In Simon Stevin (1548-1620) L'emergence de la nouvelle science, Catalogue Bibliothèque Royale Albert I, Bruxelles, (17-09-2004/30-10-2004). Turnhout: Brepols, 2004.
- Heuvel, Charles van den. 'De Huysbou': A reconstruction of an unfinished treatise on architecture, town planning and civil engineering by Simon Stevin. Amsterdam: KNAW Edita, 2005.
- Heuvel, Charles van den, "De vesting als mathematisch en cultureel kennissysteem. Het onderwijs in de vestingbouw aan hovelingen, kooplui en ambachtslieden in de Hollandse Republiek (17e eeuw)," Scientiarum Historia 32 (2006): 99-117.
- Heuvel, Charles van den, " 'As the Author Intended': Transformation of the Unpublished Writings and Drawings of Simon Stevin (1548-1620)." In Translating Early Modern Science, edited by Sietske Fransen, Niall Hodson and Karl A.E. Enenkel, 119-153. Leiden: Brill Publishers, 2017.
- Heuvel, Charles van den, "Simon Stevin's Age of the Sages. In Search of an Alternative Renaissance: Exploring Scientific Methods Based on Pre-Classical Authorities, Empirical Data and Pure Languages." In Rethinking Stevin, Stevin Rethinking. Constructions of a Dutch Polymath, edited by Karel Davids, Fokko Jan Dijksterhuis, Rienk Vermij and Ida Stamhuis, 206-233. Leiden/Boston: Brill, 2020.
- Heuvel, Charles van den, " 'Lust yemant sijn wetenschap te bewijsen, die toonet in een onghevalste suyvere Taal': Bredero en Stevin." In Voltreffer! Populariteit en popularisering van de Nederlandse letterkunde. Bijdragen ter gelegenheid van het emeritaat van Lia van Gemert, edited by Frans Blom, Lucas van der Deijl, Marjolein Hogenbirk, Jeroen Jansen, Oeds van Middelkoop, 32-35. Amsterdam: UvA Historische Nederlandse Letterkunde, 2020.
- Hietbrink, Henk, "Meetkunde met Frans van Schooten Junior (1615-1660)," Euclides 85/7 (2009/10): 279-282.
In Euclides, volume 85 number 7, 2009-2010, I wrote about how to use historical sources like the work of Frans van Schooten in geometric reasoning in undergraduate and graduate school:

- Hietbrink, Henk, Vestingbouw als context voor sinus-, cosinus en tangensregel. Euclides 96/6 (2021/05): 8-13.
The historical context of fortification helps to emphasize the usefulness of sine rule, cosine rule and tangent rule.

- Maanen, Jan A. van Facets of Seventeenth Century Mathematics in the Netherlands. Utrecht: Elinkwijk, 1987.
- Muller, E. and Kees Zandvliet, Admissies als landmeters in Nederland voor 1811. Alphen aan den Rijn: Canaletto, 1987.
- Raa, Frederik Jan Gustaaf ten, and François de Bas, Het Staatsche Leger. Breda: Koninklijke Militaire Akademie, 1913.
- Reinders, Reinder, " 'Van de fortificatie', in Ere Saluut. Opstellen voor mr. G. Overdiep" edited by Jan W. Boersma and Christiaan J.A. Jörg, 252-270. Groningen: Regio Projekt, 1995.
- Taverne, Ed R. M. In 't land van belofte: in de nieue stadt. Ideaal en werkelijkheid van de stadsuitleg in de Republiek 1580-1680. Maarssen: Gary Schwartz, 1978.
- Westra, Frans, "Samuel Crop, ingenieur in Staatse dienst te Aardenburg." Sporen naar het verleden. Heemkunde Kring West-Zeeuws Vlaanderen, 22 (1994) 10-16.
- Westra, Frans, "Jan Pietersz. Dou (1573-1635) Invloedrijk landmeter van Rijnland," Caert-Thresoor 13, no. 2 (1994): 37-48.
- Wiesenfeldt, Gerhardt "The 'Duytsche Mathematique': the Culture of Mathematics and the Family Network of Leiden University." In Location of Knowledge in Dutch Contexts. edited by Fokko Jan Dijksterhuis, Andreas Weber and Huib J. Zuidervaart, 40-63. Leiden: Brill, 2019.
- Winter, Pieter Jan van. Hoger beroepsonderwijs avant-la-lettre. Bemoeiingen met de vorming van landmeters en ingenieurs bij de Nederlandse universiteiten van de 17e en 18e eeuw. Amsterdam/Oxford/New York: Noord-Hollandsche Uitgevers Maatschappij, 1988.

 download larger version
download larger version