Vestingbouw

PDF Euclides: Vestingbouw als context voor sinus-, cosinus- en tangensregel

Handout

Een handout is ontwikkeld voor de workshop Vestingbouw op de VVWL studiedag van 9 november 2024.

PDF handout 2024 VVWL

Een handout is ontwikkeld voor de workshop Vestingbouw op de Fontys studiedag van 15 maart 2024.

PDF handout 2024 FLOS

Een handout is ontwikkeld voor de workshop Vestingbouw op de NVvW studiedag van 7 november 2020.

Bij iedere opdracht staat een tekening. De tekeningen komen uit de boeken die geschreven zijn door bovenstaande personen. Soms was enige beeldbewering noodzakelijk om een tekening leesbaar te maken. Vaak zijn extra punten en labels toegevoegd om de opdrachten eenduidig te formuleren.

De afmetingen zijn meestal uitgedrukt in Rijnlandse roeden, een oude lengtemaat. Omgerekend is die 3,767 meter lang. De Rijnlandse roede werd meestal onderverdeeld in 12 voet. Een voet is dan 31,39 cm lang. Een vierkante roede is één roede breed bij één roede lang, oftewel 14,2 m2. Een andere oppervlaktemaat is de morgen. Een morgen is 600 vierkante roeden. Omgerekend is dat ongeveer 8520 m2 en dat is iets minder dan een hectare.

Alle opdrachten in deze handout zijn gebaseerd op een regelmatige vijfhoek, maar sommige auteurs beschrijven alle veelhoeken, van de vierhoek tot en met twaalfhoek. In hun boeken is stof genoeg voor nog tientallen verrassende opdrachten.

PDF handout 2020

uitwerkingen in GeoGebra

Terminologie

Vestingbouw heeft zijn eigen terminologie. Kun jij in de tekening de volgende onderdelen aanwijzen?

Courtine
Flank
Face
Keel
Hoofdlijn
Strijklijn
Defensielijn

antwoord op deze vraag

Opdrachten

Opdracht 1: Goldmann

Opdracht 2: Stevin

Opdracht 3: Alghisi

Opdracht 4: Metius

Opdracht 5: van Schooten

Opdracht 6: Cellarius

Opdracht 7: Marolois

Nikolaus Goldmann (1611-1665)

Hiernaast staat een tekening uit het boek La nouvelle fortification van Nikolaus Goldmann uit 1645. Hij was van Duitse origine en gaf lang en verdienstelijk privelessen in Leiden in de tijd dat de familie Van Schooten doceerde aan de Duytsche Mathematicque. Jeroen Goudeau is gepromoveerd op het werk van Goldmann.

Jeroen Goudeau: Nicolaus Goldmann (1611-1665) en de wiskundige architectuurwetenschap

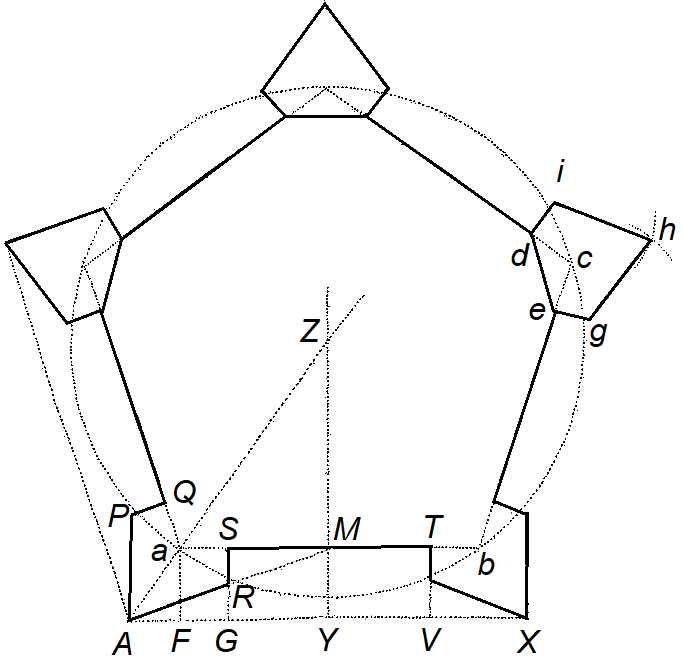
Opdracht 1 Nikolaus Goldmann (1611-1665)

In de tekening hiernaast is lijnstuk ab de zijde van de veelhoek en lijnstuk AX is de afstand tussen de punten van twee naastgelegen bolwerken. Lijnstuk AR de face. Een waarschuwing is op zijn plaats: de tekening wekt de suggestie dat lijnstuk AM de strijklijn is, maar de strijklijn komt niet precies in het midden uit. Dicht bij punt M ligt N en de strijklijn is lijnstuk AN.

Construeer op schaal een symmetrische vijfhoekige vesting op de manier van Nikolaus Goldmann:

de formule voor de bolwerkhoek is 15° meer dan de helft van de omtrekshoek, met een maximum van 90°
de courtine, ST, de wal tussen de beide flanken, is 40 roede
de flanken, RS, staan loodrecht op de courtine en zijn 6,67 roede lang
Goldmann rekende in voeten. Daarvan gaan er 12 in een roede, Voor de overzichtelijkheid is op deze webpagina alles in roeden uitgedrukt
de kelen, aS en Tb, in het verlengde van de courtine, zijn ieder 9,16 roede lang
de strijklijn, AN, het verlengde van de face snijdt de courtine bijna halverwege
Punt N ligt vlak bij punt M

Bereken:

de grootte van de bolwerkhoek PAR van een punt van een bolwerk
de afstand AX tussen de punten van twee naastgelegen bolwerken
de lengte van de strijklijn AN
de lengte van de defensielijn AT
de lengte van de nevenflank NT
de oppervlakte van een bolwerk, (veelhoek eghid)

Officieel is een bastion een vijfhoek en is lijnstuk de de keel, maar wiskundig ingestelde schrijvers als Goldmann werkten liever met zijden cd en ce als keel.

Tip: maak eerst een tekening met geogebra en gebruik de uitkomsten om je antwoorden te controleren.
Waarschuwing: punt R ligt beslist niet op de cirkel, maar iets daar buiten.

In GeoGebra is een uitwerking gemaakt van deze opdracht. Daar kun je variëren met andere veelhoeken.

aantal zijden:	4	5	6	7	8	9	10
courtine ST:	40	40	40	40	40	40	40
flank RS:	5,0	6,7	7,5	8,3	9,2	10,0	10,0
keel aS:	9,1	9,2	9,7	10,2	10,5	10,7	11,2

La nouvelle fortification

E-RaRa

Op de Zwitserse website van ETH Zürich staat een schat aan oude drukken.

Wikipedia

Op wikipedia staan veel artikelen over vestingbouw tijdens de Tachtigjarige_Oorlog.

Oud-Nederlands vestingstelsel

Lijst van vaktermen in de vestingbouwkunde

Bastion

Simon Stevin (1548-1620)

Simon Stevin was een vernufteling: een uitvinder en een wetenschapper. Hij gooide twee loden ballen met verschillend gewicht van de toren van Delft. Volgens de traditie moest de zware bal het snelst vallen. Stevin beweerde dat ze even snel zouden vallen. Simon Stevin leerde Europa rekenen met decimale breuken: "De Thiende". Hij schreef over wiskunde, natuurkunde, techniek en de Nederlandse taal. Van hem zijn de woorden "wisconst", "middellini", "omtreck" en "euewydighe". Hij was leraar van Prins Maurits en kwartiermeester in het Staatse leger. Stevin schreef in 1600 het programma voor de Ingenieursschool in Leiden. Daar gaven Frans van Schooten Senior en Frans van Schooten Junior en Pieter van Schooten les.

Opdracht 2 Simon Stevin (1548-1620)

Simon Stevin schreef in 1594 als een van de eersten een helder boek over vestingbouw in begrijpelijk Nederlands. Hij gaf precies aan hoe hoog en breed de wallen en bastions moesten zijn en hoe breed en hoe diep de gracht. Onderstaande tekening komt uit zijn boek Sterctenbovwing. In Google Forms staan drie vragen. De eerste vraag gaat over de hoogte van de bastions, de tweede over de diepte van de gracht. De derde vraag is waar in Nederland dit voorstel gerealiseerd is.

Google Forms

Lijn AP is het grondniveau. Punt R is de bovenkant van de borstwering van het bastion. Hoe hoog is punt R boven het grondniveau?
Lijn AP is het grondniveau en punt X markeert het waterpeil. Hoe diep is punt Y, de bodem van de gracht, in meters onder grondniveau
Welke steden in Nederland kwamen in aanmerking voor de bouw van een vesting die Simon Stevin beschreef?

Simon Stevin geeft op bladzijde 11 de volgende afmetingen in voeten en herhaalt deze op bladzijde 28.

de straal van de zeshoek is 1000 voet
de lengte van de omtrekszijde BC is 1000 voet
de lengte van de linkerkeel CK is 180 voet en die van rechterkeel BH ook
de lengte van de courtine HK is 640 voet
de flank staat loodrecht op de courtine
de lengte van de linker flank KO is 140 voet en die van de rechterflank HM ook
de breedte van de borstwering HR is 20 voet
de halve breedte van de linker borstwering KV is 10 voet en die van de rechter HT ook
de strijklijn VZ valt samen met de defensielijn TY

Na 1600 vond men dat een bolwerk niet te spits maar zeker niet stomp mocht zijn. Ook vond men dat de defensielijn niet langer dan 60 roeden (720 voeten) mag zijn. Opdracht is om met berekeningen vast te stellen of het ontwerp van Stevin aan deze voorwaarden voldoet.

de lengte van de defensielijn VZ is kleiner dan 720 voet
de grootte van de bolwerkshoek MZN is kleiner dan 90°

Uiteraard valt er meer te berekenen, bijvoorbeeld de lengte van de hoofdlijn BZ.

Google Books: Sterctenbovwing, bladzijde 18

3D print

Met een 3D printer is een schaalmodel gemaakt van een zeshoekige vesting. Stevin stelde zelf voor dat docenten instructie gaven met een houten voorbeeld. Met een gespannen draad konden ze met dat model de strijklijnen en defensielijn zichtbaar maken.

Sterctenbovwing

Het boek Sterctenbovwing is digitaal beschikbaar. Een wetenschapelijke uitgave staat op de website van het KNAW.

google books

KNAW

BSB-MDZ

Opdrachten

Opdracht 1: Goldmann

Opdracht 2: Stevin

Opdracht 3: Alghisi

Opdracht 4: Metius

Opdracht 5: van Schooten

Opdracht 6: Cellarius

Opdracht 7: Marolois

Alghisi (1523-1573)

Galasso Alghisi da Carpi was een Italiaans architect uit de Renaissance. Hij vond dat vestingbouw niet overgelaten kon worden aan militairen en schreef een boek hoe een vesting met bastions er uit moest zien.

Opdracht 3 Galasso Alghisi da Carpi (1523-1573)

Alghisi construeerde een vesting met als grondvorm een regelmatige vijfhoek met geknikte courtines en met vijf bolwerken. In deze opdracht is de oppervlakte van de binnenste vijfhoek exact één morgen, dat wil zeggen precies 600 vierkante roeden (ongeveer 8520 m²). Bereken de grootte van alle relevante hoeken, waaronder:

de bolwerkhoek A
de grootte van de hoek L van de knik in de courtine

Bereken de lengte in roeden van:

face CW
courtine LV
flank VW

Eenvoudiger is de opdracht met gegeven KL = 20. Doorzetters rekenen ook de grootte van de defensiehoek en de lengte van de defensielijn uit.

In GeoGebra is een uitwerking gemaakt van deze opdracht.
Variaties zijn mogelijk. Geef bijvoorbeeld een andere lengte of een andere oppervlakte.

Galasso Alghisi, Delle fortificationi libri tre, Venice 1570

Delle fortificationi libri

In Delle fortificationi libri beschrijft Alghisi de vijfhoek tot en met de een-en-twintig hoek.

Opdrachten

Opdracht 1: Goldmann

Opdracht 2: Stevin

Opdracht 3: Alghisi

Opdracht 4: Metius

Opdracht 5: van Schooten

Opdracht 6: Cellarius

Opdracht 7: Marolois

Adriaan Metius Adriaan Metius (1571-1635)

Adriaan Adriaansz. Metius (Alkmaar, 1571 - Franeker, 1635) studeerde wiskunde in Franeker en Leiden. Zijn vader was Adriaen Anthonisz (1541-1620), vestingbouwkundige, cartograaf, wiskundige en burgemeester van Alkmaar. Adriaen Anthonisz werkte volgens de principes van het oud-Nederlands vestingstelsel. Zijn werkterrein was heel Noord-Nederland. In Alkmaar is in 1997 een standbeeld onthuld van Adriaen Anthonisz aan het werk met een hoekmeter.
Vanaf 1598 was Metius verbonden aan de Universiteit van Franeker als hoogleraar en gaf les in navigatieleer, landmeetkunde, militaire techniek en astronomie. Metius heeft een groot aantal boeken geschreven over wiskunde en toepassingen als astrolabes, kalenders, passers, of tabellen over zonsdeclinatie.

Wikipedia: Adriaen Anthonisz

Wikipedia: Adriaan Metius

Opdracht 4 Adriaan Metius (1571-1635)

Metius construeerde een vesting met vijf bolwerken met als grondvorm een regelmatige vijfhoek met zijde NO = 540 voeten, oftewel 45 roeden. De verhoudingen tussen de lengtes waren volgens zijn vader:

Keel : Zijde = AN : NO = 2 : 9
Flank : Zijde = BD : NO = 1 : 6

Metius gebruikt de formule dat de bolwerkhoek gelijk is aan twee derde van de omtrekshoek, maar hoogstens 90°.

Bereken:

de grootte van de omtrekshoek BOE
de grootte van de bolwerkhoek DHP
de lengte van de face DH
de lengte van de defensielijn AH

In GeoGebra is een uitwerking gemaakt van deze opdracht. Daar kun je variëren met andere veelhoeken.

aantal zijden:	5	6	7	8	9	10
zijde NO:	540	648	648	648	648	648

Fortificatie ofte stercken-bouwinghe

Adriaan Metius schreef het boek, Fortificatie ofte stercken-bouwinghe, waarin hij zeer nauwkeurig uitlegde hoe zijn vader Adriaen Anthoniszn. ontwerpen voor vestingen berekende.

google books

Opdrachten

Opdracht 1: Goldmann

Opdracht 2: Stevin

Opdracht 3: Alghisi

Opdracht 4: Metius

Opdracht 5: van Schooten

Opdracht 6: Cellarius

Opdracht 7: Marolois

Pieter van Schooten (1634-1679)

Pieter van Schooten is de minder bekende halfbroer van Frans van Schooten Jr. Pieter van Schooten was van 1660 tot 1679 de derde uit de familie van Schooten die les gaf aan de Duytsche Mathematique, onder andere over vestingbouw. Ook heeft hij de steden Utrecht en Leiden geadviseerd over hun vestingwerken. Na de dood van Frans Jr in 1660 heeft Pieter zijn lessen aan de Duytsche Mathematicque overgenomen.

Opdracht 5 Pieter van Schooten (1634-1679)

Pieter van Schooten construeerde een regelmatig vijfhoekige vesting met bolwerkafstand CI = 60 roeden. Hij berekende de bolwerkhoek met de formule een derde van de omtrekshoek plus 30°. De lengte van de hoofdlijn AC verhoudt zich tot de zijde AB als 1 : 3. De lengte van de keel AO verhoudt zich tot de zijde AB als 1 : 5.

Bereken de lengte van:

Face CE
Flank EO
Courtine DO
Hoofdlijn AC
Keel AO
Strijklijn CR
Defensielijn DC

Tip: bereken eerst alle relevante hoeken, bijvoorbeeld omtrekshoek, de bolwerkhoek en de strijkhoek.

In GeoGebra is een uitwerking gemaakt van deze opdracht. Daar kun je variëren met andere veelhoeken. Pieter houdt in zijn manuscript vast aan bolwerksafstand 60 roeden voor iedere veelhoek.

Architectvra Militaris, Oder Gründtliche Vnderweisung der heuttiges tages so wohl in Niederlandt als andern örttern gebräuchlichen Fortification Oder Vestungsbau

Manuscripten

De tekening hiernaast komt uit het Leidse handschrift BPL 1993. Van Pieter van Schooten zijn enkele manuscripten bewaard in de universiteitsbibliotheken van Groningen en Leiden.

Leiden: BPL 1993

Opdrachten

Opdracht 1: Goldmann

Opdracht 2: Stevin

Opdracht 3: Alghisi

Opdracht 4: Metius

Opdracht 5: van Schooten

Opdracht 6: Cellarius

Opdracht 7: Marolois

Andreas Cellarius (1595-1665)

Van Cellarius is het boek "Architectura militaris" uitgegeven in 1645 bij Jodocum Jansonium in het Duits. Cellarius vermeldt ook de vertalingen van de begrippen in het Nederlands, Frans en Latijn. Cellarius studeerde in Heidelberg, huwde in 1625 in Amsterdam, en werd in 1637 rector van de Latijnse school in Hoorn. Hij overleed in 1665, vijf jaar na de uitgave van zijn prachtige "Harmonia Macrocosmica".

Flandrica: Harmonia Macrocosmica

Opdracht 6 Andreas Cellarius (1595-1665)

Cellarius construeerde een regelmatige vijfhoek met courtine CG = 36, flank CI = 9, face IM = 24 roeden. De bolwerkhoek werd berekend met de formule twee derde van de omtrekshoek, maar hoogstens 90°.

Deze opdracht gaat over het gebruik van de tangensregel als alternatief voor de cosinusregel. Bereken met de tangensregel de grootte van de defensiehoek.

Bereken:

Lengte keel BC
Lengte strijklijn FM
Defensiehoek CGM met de tangensregel
Lengte defensielijn GM

In GeoGebra is een uitwerking gemaakt van deze opdracht. Daar kun je variëren met andere veelhoeken. Achter in zijn boek geeft Cellarius een aantal tabellen met afmetingen voor verschillende toepassingen. Soms is er sprake van vergrotingen. Zo toont hij tabellen voor bolwerksafstanden van 35 tot en met 70 roeden, oplopend met 5 roeden. De basisuitvoering heeft steeds courtine CG = 36 en face IM = 24 roeden, maar flank CI = 6 bij een vierhoek, oplopend tot 12 roeden bij een tienhoek.

Wikipedia: bewijs tangensregel

Tangensregel

In iedere willekeurige driehoek ABC met hoeken α, β en γ en zijden a, b en c geldt de tangensregel:

a − b	=	tan(½(α − β))
a + b	tan(½(α + β))

Samuel Marolois (1572-1627)

Marolois is de auteur van een aantal boeken over wiskunde, perspectief tekenen en vestingbouw. In het Franstalige boek "Fortification ou architectvre militaire" uitgegeven in 1615 bij Hondius, staan een groot aantal variaties om te rekenen aan de afmetingen van een vestuingwerk. Marolois was ingenieur en wiskundige. Met een aanbeveling van Prins Maurits solliciteerde hij in 1611 naar een betrekking aan de Duytsche Mathematique, maar de positie ging naar Frans van Schooten Senior.

Opera mathematica ou oeuvres mathématicques : traictans de géometrie, perspective, architecture et fortification ausquels sont aioints les fondements de la perspective & architecture de I: Vredm. Vries, augmentée & corrigée en divers endroicts par le mesme auteur (1614/1615)

Fortification ou architecture militaire tant offensive que deffensive / supportée et dessignée par Samuel Marolois (1627)

Architectura: overzicht

Omnia: overzicht

Molhuysen: sollicitatie

Opdracht 7 Samuel Marolois (1572-1627)

Marolois construeerde een regelmatige vijfhoek met centrum O en zijde FM. Gegeven is de lengte van de strijklijn AB = VN = 50 en de lengte van de flank DE = 9 en de grootte van de bolwerkshoek ∠CBE = 72°.

NB: Marolois vergat in 1615 te vermelden dat tweede flank AG = DN = 5, maar herstelde dat in de editie van 1627.

Bereken de lengte van de verschillende onderdelen:

face BE
courtine DG
keel DF = GM
zijde FM
afstand tussen bolwerkspunten BV

Bereken ook de grootte van de volgende hoeken:

strijkhoek ∠BAC
defensiehoek ∠MDV

Extra:

Onderzoek of de suggestie juist is dat de figuur een rechthoek is met punt OONV recht is.

Onfderstaande tekening is een bewerking van tekening met nummer 7 en staat zowel in de editie van 1614 als die ban 1627.

Opdrachten

Opdracht 1: Goldmann

Opdracht 2: Stevin

Opdracht 3: Alghisi

Opdracht 4: Metius

Opdracht 5: van Schooten

Opdracht 6: Cellarius

Opdracht 7: Marolois

Learning Places

Charles van de Heuvel presenteerde Servants of Mathesis. Early 17^th-century teaching in geometry and fortification and digital mathematics education tijdens de hybride conferentie Learning Places in 2022 in Lissabon. Onderdeel daarvan is mijn vergelijking van tientallen calculaties door vestingbouwers uit de 17^de eeuw.

TechNet Learning Places: Mijn vergelijking van calculaties

Publicaties Stichting Menno van Coehoorn

Vergelijking van de opdrachten

In onderstaande tabel is een vergelijking van de opbouw van de besproken opdrachten. op deze webpagina staan er slechts vijf, maar in mijn onderzoek heb ik de aanpak van vijftien auteurs bestudeerd en ook een aantal manuscripten die mogelijk gediend hebben als college voorbereiding dan wel als collegedictaat of college aantekeningen. Deze manuscripten staan vol goniometrische berekeningen. In de besproken opdrachten zijn er twee verschillende formules voor de bolwerkhoek, maar het is verbazingwekkend hoeveel variatie wiskundigen wisten aan te brengen in deze formule.

	Nikolaus Goldmann	Adriaan Metius	Pieter van Schooten	Andreas Cellarius
bolwerkhoek		formule	formule	formule
Zijde		gegeven	verhouding
Courtine	gegeven			gegeven
Flank	gegeven	verhouding		gegeven
Keel	gegeven	verhouding	verhouding
Face				gegeven
Hoofdlijn			verhouding
Strijklijn	gegeven
Defensielijn
Afstand tussen bolwerkpunten			gegeven

Terminologie verdedigingswerken

De Stichting Menno van Coehoorn heeft een overzichtelijk boek gepubliceerd over de terminologie van verdedigingswerken.

Stichting Menno van Coehoorn

Terminologie

In de opdrachten worden een aantal begrippen gehanteerd:

Saillant is de voorste punt van het bolwerk
Courtine is de wal ingesloten tussen twee bolwerken
Flank is de zijkant van het bolwerk dat uitkijkt op de courtine
Flankhoek is de hoek tussen de courtine en de flank, vaak recht, soms stomp
Face is de voorkant van het bolwerk
bolwerkhoek is de hoek tussen beide facen
Schouderhoek is de stompe hoek tussen flank en face
Keel is het verlengde van de courtine
Keel plus courtine plus keel maken samen de zijde van de veelhoek
(nb: voor niet-wiskundigen is de keel de lijn tussen de flankhoeken)
Keelhoek of omtrekshoek is de hoek tussen beide keellijnen of zijdes
Hoofdlijn is de lijn van de saillant naar de keelhoek
Strijklijn is de lijn van de saillant langs de face verlengd tot de courtine
Strijkhoek is de scherpe hoek tussen courtine en strijklijn
Defensielijn is de lijn van flankhoek tot saillant
Defensiehoek is de scherpe hoek tussen courtine en defensielijn

In de zeventiende eeuw waren de begrippen strijklijn en defensielijn gangbaar. Tegenwoordig spreekt men van strijkende defensielijn en bestendige defensielijn.

Animatie terminologie