www.fransvanschooten.nl

XIV

Van een vierhoekig stuk land ABCD is op zijde AD het punt E bepaald.
Lijn CE is evenwijdig aan zijde AB.
Op lijn CE ligt punt F zodanig dat lijn DF evenwijdig is aan zijde BC.
Enkele afmetingen zijn bekend: AB = 15, EF = 2 en FC = 7

Waar op AD ligt punt G waarvan de lijn GH, evenwijdig aan zijde AB, vierhoek ABCD in twee even grote stukken deelt?

tip

  1.   

    • tip

      Verdeel de veelhoek in driehoeken en bereken de relatieve grootte van de oppervlaktes.

antwoord

  1.   

    • antwoord


      opp. ∆ABK : opp. ∆ECK = AB² : EC²

      opp. ∆ABK : opp. ∆GHK = AB² : GH²

      opp. ∆ABK : opp. ∆DCK = EK : DK = EC : CF

      opp. ∆ABK = opp. ∆DCK ×AB²
      EC × CF

      opp. ∆GHK = opp. ∆DCK ×GH²
      EC × CF

      opp. ABHG = opp. GHCD

      opp. ∆ABK − opp. ∆GHK = opp. GHK − opp. ∆DCK

      opp. ∆ABK + opp. ∆DCK = 2 × opp. GHK

      opp. ∆DCK ×AB²+ opp. ∆DCK = 2 × opp. ∆DCK ×GH²
      EC × CFEC × CF

      AB² + EC × CF = 2 × GH²

      invullen AB = 15 en EF = 2 en FC = 7 geeft GH = 12

opdracht 13

opdracht 15

 


Hiernaast staat een ander, vergelijkbaar probleem. Vierhoek ABCE is een trapezium met zijde AB evenwijdig aan zijde CE. Gevraagd wordt naar de lengte van lijn GH, evenwijdig aan lijn AB en lijn CE dat de vierhoek in twee delen met even grote oppervlakte deelt.
In het verlengde van zijde AE en zijde BC ligt snijpunt K.
In deze figuur geldt dat EK : EC = GK : GH = AK : AB.

zodat AK = GK ×AB
GH

zodat EK = GK ×EC
GH

Vierhoek ABHG moet even groot zijn als vierhoek GHCE, dus AG (AB + GH) = GE (GH + EC).
AG = AK − GK = GK (AB− 1)
GH

GE = GK − EK = GK (1 −EC)
GH

Substitutie geeft
GK (AB− 1) (AB + GH) = GK (1 −EC) (GH + EC).
GHGH

en dan GK (AB − GH) (AB + GH) = GK (GH − EC) (GH + EC) en dan AB² − GH² = GH² − EC²
dus 2 × GH² = AB² + EC² en daaruit volgt de gevraagde lengte van lijnstuk GH.
 


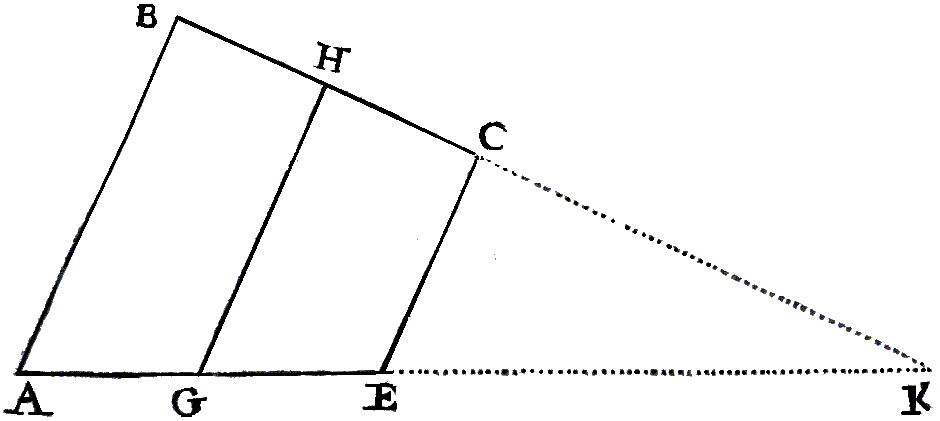
top