Verdeel een lijn in twee gelijke stukken

Hieronder staan alternatieve uitwerkingen voor de opdracht een lijn te verdelen in twee gelijke stukken.

zwaartelijn
Menelaos
Parallellogram

Opdracht 126 met Zwaartelijn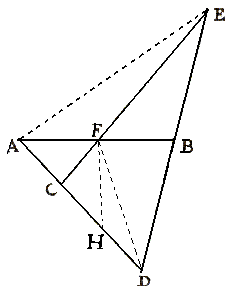

1. Leg uit waarom de oppervlakte van ∆ABE even groot is als de oppervlakte van ∆ABD.
    
   Antwoord: Een zwaartelijn verbindt een hoekpunt met het midden van de tegenoverliggende zijde. Eigenschap van de zwaartelijn is dat het een lijn is die een driehoek in twee even grote oppervlaktes deelt.
   Volgens de constructie is BD = BE. Punt B is daarom het midden van DE. In ∆ADE is lijn AB dus een zwaartelijn. Gevolg is dat de oppervlakte van ∆ABE even groot is als die van ∆ABD.
2. Leg uit waarom de oppervlakte van ∆DBF even groot is als de oppervlakte van ∆EBF.
    
   Antwoord: De driehoeken DBF en EBF hebben even grote basis op dezelfde lijn DBE want BD = BE met dezelfde top F. Gevolg is dat ze de zelfde hoogtelijn uit F hebben. Beide driehoeken hebben dus dezelfde hoogte. Driehoeken met even grote basis en even grote hoogte hebben een even grote oppervlakte. Daarom is de oppervlakte van ∆DBF even groot als die van ∆EBF.
3. Leg uit waarom de oppervlakte van ∆ACF even groot is als de oppervlakte van ∆CHF als van ∆HDF.
    
   Antwoord: Driehoeken met zelfde top en een even lange basis op een zelfde lijn zijn even groot.
   In dit geval hebben de driehoeken ACF en CHF en HDF dezelfde top in F en een even grote basis op dezelfde lijn, want AC = CH = HD. Daarom is hun oppervlakte even groot.
4. Hoeveel groter is de oppervlakte van ∆CDE dan die van ∆ACE?
    
   Kort Antwoord: Driehoeken met zelfde top en een even lange basis op een zelfde lijn zijn even groot.
   In dit geval betekent dat dat de drie driehoeken ∆ACE, ∆CHE en ∆HDE even groot zijn. Gevolg is dat ∆ACE de helft is van ∆CDE want dat is de som van de even grote ∆CHE en ∆HDE. Daarom is de oppervlakte van ∆CDE het dubbele van ∆ACE.
    
   Lang Antwoord: Omdat de oppervlakte van ∆ABD even groot is als die van ∆ABE en die van ∆DBF als die van ∆EBF is die van ∆AEF even groot als die van ∆ADF, te weten driemaal die van ∆ACF. Gevolg is dat de oppervlakte van ∆ACE vier keer die van ∆ACF is.
   Lijn CFE verdeelt ADE in twee driehoeken, ACE en CDE, met basis op dezelfde lijn ACD met CD het dubbele van AC en zelfde top E. Daarom is de oppervlakte van ∆CDE het dubbele van ∆ACE.
5. Hoeveel groter is de oppervlakte van ∆BDF dan die van ∆ACF?
    
   Antwoord: De oppervlakte van ∆ACE is vier maal de oppervlakte van ∆ACF. De oppervlakte van ∆CDE is twee maal die van ∆ACF en tweemaal die van ∆BDF, maar ook het dubbele van ∆ACE en dus acht maal die van ∆ACF. Hieruit volgt dat de oppervlakte van ∆BDF driemaal zo groot is als die van ∆ACF.
6. Waarom is DF een zwaartelijn?
    
   Antwoord: Een zwaartelijn verbindt een hoek met het midden van de tegenoverliggende zijde en verdeelt een driehoek in twee even grote oppervlaktes.
   In dit geval is de oppervlakte van ∆ADF driemaal die van ∆ACF. Daarom is ∆ADF even groot als ∆BDF. Een lijn uit de top die een driehoek deelt in twee even grote oppervlaktes is per definitie een zwaartelijn. Dat betekent dat lijn DF een zwaartelijn is van ∆ABD.
7. Verklaar waarom AF = BF.
    
   Antwoord: In een driehoek verbindt een zwaartelijn een hoekpunt met het midden van de zijde er tegenover. Punt F van zwaartelijn DF in ∆ABDis dus het midden van zijde AB. Dus zijn de lijnstukken AF en BF even lang.
   Conclusie is dus dat AF = BF.

Verantwoording

Met dank aan Q. Puite voor deze originele uitwerking.
Q. Puite is mede-organisator van de Nederlandse Wiskunde Olympiade.
Stichting Nederlandse Wiskunde Olympiade .
Ook de uitwerking met Menelaos is van hem afkomstig.