
 De hoogtelijn in de gelijkbenige driehoek met zijden 9 en 9 en basis 6 verdeelt een zijde in 7 en 2.
De hoogtelijn in de gelijkbenige driehoek met zijden 9 en 9 en basis 6 verdeelt een zijde in 7 en 2.

 De hoogtelijn in de gelijkbenige driehoek met zijden 9 en 9 en 12 verdeelt de basis in 1 en 8.
De hoogtelijn in de gelijkbenige driehoek met zijden 9 en 9 en 12 verdeelt de basis in 1 en 8.
Een hoogtelijn uit een hoek staat loodrecht op de tegenoverliggende zijde.
Daarom verdeelt een hoogtelijn een driehoek in twee rechthoekige driehoeken.
Zo onstaan drie paren van rechthoekige driehoeken.
Iedere rechthoekige driehoek heeft als zijden een zijde van de oorspronkelijke driehoek, een hoogtelijn en een deel van een andere zijde van de oorspronkelijke driehoek.
In de schets staat een driehoek met zijden 29,575 en 34,125 en 31,850.
De hoogtelijnen zijn 27,3 en 29,4 en 25,48.
Het getal in het rondje in de schets van Frans van Schooten geeft de plaats van de komma aan in het getal.
Zo betekent 3185  het getal 31,85.
het getal 31,85.
De rechthoekige driehoeken zijn dan:
| hoogtelijn | rechthoekszijde | lange zijde |


|
| 27,300 | 11,375 | 29,575 | |
| 27,300 | 20,475 | 34,125 | |
| 29,400 | 12,250 | 31,850 | |
| 29,400 | 17,325 | 34,125 | |
| 25,480 | 15,015 | 29,575 | |
| 25,480 | 19,110 | 31,850 | |
De middelste kolom met rechthoekszijden zijn samen paarsgewijs even lang als de zijden van de oorspronkelijke driehoek: 11,375 + 20,475 = 31,85
Rechthoekige driehoeken met zijde 96:
| 96 | 28 | 100 | 4 keer 24 7 25 |
| 96 | 40 | 104 | 8 keer 12 5 13 |
| 96 | 72 | 120 | 24 keer 4 3 5 |
| 96 | 110 | 146 | 2 keer 55 48 73 (niet genoemd) |
| 96 | 128 | 160 | 32 keer 4 3 5 |
| 96 | 180 | 204 | 12 keer 15 8 17 |
| 96 | 247 | 265 | (niet genoemd) |
| 96 | 280 | 296 | 8 keer 35 12 37 |
| 96 | 378 | 390 | 6 keer 63 16 65 |
| 96 | 572 | 580 | 4 keer 143 24 145 |
| 96 | 765 | 771 | 3 keer 255 32 257 |
| 96 | 1150 | 1154 | 2 keer 575 48 577 |

 Een driehoek met zijden 45,63 en 38,61 en 70,2 laat zich met een hoogtelijn delen
in de rechthoekige driehoeken met zijden 23,166 en 39,312 en 45,630 en met zijden 23,166 en 30,888 en 38,610.
Een driehoek met zijden 45,63 en 38,61 en 70,2 laat zich met een hoogtelijn delen
in de rechthoekige driehoeken met zijden 23,166 en 39,312 en 45,630 en met zijden 23,166 en 30,888 en 38,610.
Deze driehoek laat zich verlengen tot de rechthoekige driehoeken met zijden 42,12 en 56,16 en 70,20 en die met zijden 35,64 en 60,48 en 70,200
met behulp van de rechthoekige driehoeken met zijden 42,12 en 17,55 en 45,63 en die met zijden 35,64 en 14,85 en 38,61.
NB: Dit zijn allemaal exacte getallen en geen afrondingen!

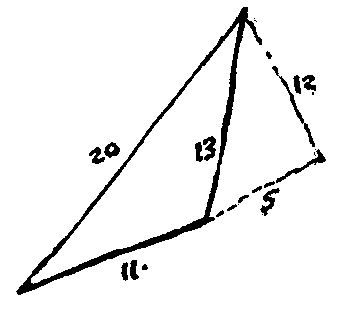 Een driehoek met zijden 11 en 13 en 20 laat zich verlengen tot een rechthoekige driehoek met zijden 12 en 16 en 20,
de vergroting van driehoek 3, 4 en 5.
Een driehoek met zijden 11 en 13 en 20 laat zich verlengen tot een rechthoekige driehoek met zijden 12 en 16 en 20,
de vergroting van driehoek 3, 4 en 5.

 Een driehoek met zijden 715 en 845 en 1300 laat zich met een hoogtelijn delen
in de rechthoekige driehoeken met zijden 429 en 572 en 715 en die met zijden 429 en 728 en 845.
Een driehoek met zijden 715 en 845 en 1300 laat zich met een hoogtelijn delen
in de rechthoekige driehoeken met zijden 429 en 572 en 715 en die met zijden 429 en 728 en 845.
Deze driehoek laat zich verlengen tot de rechthoekige driehoeken met zijden 780 en 1040 en 1300 en die met zijden 660 en 1120 en 1300
met behulp van de rechthoekige driehoeken met zijden 325 en 780 en 845 en die met zijden 275 en 660 en 715.

 Een driehoek met zijden 7 en 15 en 20.
Deze driehoek laat zich verlengen tot de rechthoekige driehoeken met zijden 12 en 16 en 20
en die met zijden 53/5 en 191/5 en 20
met behulp van de rechthoekige driehoeken met zijden 9 en 12 en 15
en die met zijden 41/5 en 53/5 en 7.
Een driehoek met zijden 7 en 15 en 20.
Deze driehoek laat zich verlengen tot de rechthoekige driehoeken met zijden 12 en 16 en 20
en die met zijden 53/5 en 191/5 en 20
met behulp van de rechthoekige driehoeken met zijden 9 en 12 en 15
en die met zijden 41/5 en 53/5 en 7.

 De hoogtelijn in de rechthoekige driehoek met zijden 15 en 20 en 25 verdeelt de basis in 9 en 16.
Zo ontstaan de rechthoekige driehoeken met zijden 9 en 12 en 15 en die met zijden 12 en 15 en 20.
Bijzonder is dat deze driehoeken gelijkvormig zijn.
Ze zijn allemaal een vergroting van de rechthoekige driehoek met zijden 3 en 4 en 5.
De hoogtelijn in de rechthoekige driehoek met zijden 15 en 20 en 25 verdeelt de basis in 9 en 16.
Zo ontstaan de rechthoekige driehoeken met zijden 9 en 12 en 15 en die met zijden 12 en 15 en 20.
Bijzonder is dat deze driehoeken gelijkvormig zijn.
Ze zijn allemaal een vergroting van de rechthoekige driehoek met zijden 3 en 4 en 5.

 Een driehoek met zijden 35 en 75 en 100 laat zich met een hoogtelijn delen
in de rechthoekige driehoeken met zijden 21 en 28 en 35 en die met zijden 21 en 72 en 75.
Deze driehoek laat zich verlengen tot de rechthoekige driehoeken met zijden 28 en 100 en 96 en die met zijden 60 en 80 en 100
met behulp van de rechthoekige driehoeken met zijden 21 en 28 en 35 en die met zijden 45 en 60 en 75.
Een driehoek met zijden 35 en 75 en 100 laat zich met een hoogtelijn delen
in de rechthoekige driehoeken met zijden 21 en 28 en 35 en die met zijden 21 en 72 en 75.
Deze driehoek laat zich verlengen tot de rechthoekige driehoeken met zijden 28 en 100 en 96 en die met zijden 60 en 80 en 100
met behulp van de rechthoekige driehoeken met zijden 21 en 28 en 35 en die met zijden 45 en 60 en 75.
Frans van Schooten heeft deze driehoek niet op schaal getekend!
 Lees verder over driehoeken waarvan de hoogtelijn de overstaande zijde in twee geheeltallige stukken deelt
Lees verder over driehoeken waarvan de hoogtelijn de overstaande zijde in twee geheeltallige stukken deelt