Meetkundig Verband
Hieronder staan allemaal verschillende problemen die gaan over geheeltallige driehoeken.
Met algebra kunnen vergelijkingen over de exacte lengtes van de zijden van driehoeken opgesteld worden.
Recepten zijn beschikbaar om driehoeken met geheeltallige lengtes te maken:
|
|
|
rechthoekige driehoeken met geheeltallige zijden
44 verso
|
Rechthoekige driehoeken met geheeltallige zijden
|
Gezocht wordt naar een rechthoekige driehoek met geheeltallige zijden.
|
|
GN108
Frans van Schooten tekende op 44 verso allemaal driehoeken met rechthoekszijde b = 96.
Hij begon met het drietal ( 28 , 96 , 100 ),
stopte bij het drietal ( 1150 , 96 , 1154 ),
maar had door kunnen gaan tot het drietal ( 2303 , 96 , 2305 ).
Dit drietal staat voor de grootste driehoek met rechthoekszijde b = 96.
Met algebra kan aangetoond worden dat er geen geheeltallige rechthoekige driehoeken zijn met geheeltallige zijde c > 2305.
Op 45 recto staan allemaal driehoeken met rechthoekszijde b = 60.

Frans van Schooten tekende in één figuur tien driehoeken. Ze zijn niet op schaal getekend.
Historie
In de loop der eeuwen zijn over geheeltallige rechthoekige driehoeken verschillende problemen geformuleerd.
1. Gegeven één zijde, vind de grootste driehoek.
 Lees het recept van Plato Lees het recept van Plato
2. Vind systematisch alle driehoeken.
 Lees het recept van Euclides Lees het recept van Euclides
3. Vind alle driehoeken waarvan de ene rechthoekszijde één eenheid langer is dan de andere
 Lees het recept van Fermat Lees het recept van Fermat
Vergelijkingen Grootste Driehoek
Hiernaast staat ∆ABC.
Gegeven rechthoekszijde b, gezocht wordt naar de grootste driehoek, dat wil zeggen de driehoek met de grootste oppervlakte.
Dat is de driehoek waarvan het verschil in lengte tussen langste zijde en rechthoekszijde minimaal is.
| Volgens de stelling van Pythagoras geldt in iedere rechthoekige driehoek ABC met een rechte hoek in punt c:
a² + b² = c².
De grootste driehoek heeft een spitse hoek tegenover zijde b, waardoor c > a > b.
| Als b even is, dan is b² ook even. Dus moeten a² en c² of beide even of beide oneven zijn.
Het verschil tussen c en a is dus minimaal 2.
Daarom c = a + 2.
Uit a² + b² = (a+2)²
volgt a² + b² = a² + 4a + 4
en dus dat
.
| Als b oneven is, dan is b² oneven, dan moeten a en c even en oneven zijn, dan wel oneven en even.
Het verschil tussen c en a is dus minimaal 1.
Daarom c = a + 1.
Uit a² + b² = (a+1)²
volgt dat .
|
Conclusie
Conclusie is dat als b gegeven is, dat je dan de grootste a en c uit kunt rekenen.
 recept van Plato recept van Plato
 recept van Euclides recept van Euclides
 recept van Fermat recept van Fermat
|
 
Frans van Schooten tekende in één figuur tien driehoeken. Ze zijn niet op schaal getekend.
 
|
|
Voorbeeld
De berekening voor het grootste drietal voor een driehoek met zijde b = 96 staat hieronder.
Omdat b even is, is c = a + 2.
Uit a² + b² = c² met b = 96 volgt
96² + a² = (a+2)².
Daarom is 4a = 96² − 4,
zodat a = 2303 en c = a + 2 = 2305.
|
|
Straal ingeschreven cirkel
Een bijzondere eigenschap van een geheeltallige rechthoekige driehoek is dat de straal van de ingeschreven cirkel ook geheeltallig is.
Het bewijs is gebaseerd op het recept van Euclides voor geheeltallige rechthoekige driehoeken.
 Bewijs geheeltallige straal ingeschreven cirkel Bewijs geheeltallige straal ingeschreven cirkel
| 
|
|
|
 top top
Algebra
In iedere rechthoekige driehoek met rechthoekszijden a, b en langste zijde c geldt:
a² + b² = c²
 Applet: Pythagoras Applet: Pythagoras
Fermat
Fermat heeft een recept gegeven voor rechthoekige driehoeken waarvan de rechthoekszijden slechts één verschillen.
 Recept: (a,a+1,c) Recept: (a,a+1,c)
|
rechthoekige driehoeken met geheeltallige zijden
34
|
Rechthoekige driehoeken met geheeltallige zijden
|
Gezocht wordt naar een rechthoekige driehoek met geheeltallige zijden.
|
|
Viète Opera Mathematica
Frans van Schooten kende het recept van Euclides voor Pythagoreïse drietallen.
In 1646 publiceerde hij "Viète Opera Mathematica".
Op bladzijde 34 staan de formules.
De notatie is heel anders dan de moderne algebraïsche notatie of de notatie die hij in 1659 gebruikte in zijn "Mathematische Oeffeningen".
De letter q staat voor quadratorum, kwadraat.
De lengte van de horizontale rechthoekszijde is a² − b²,
De lengte van de langste zijde is a² + b².
Het woord bis betekent het dubbele en het woord in staat voor vermenigvuldigen.
De lengte van de verticale rechthoekszijde is 2 × a × b,
afgekort tot 2ab.
Opdrachten
| Opdracht 1
|
Bewijs met de stelling van Pythagoras dat voor iedere a en b de driehoek rechthoekig is.
| | Opdracht 2
|
Hiernaast staan twee rechthoekige driehoeken BDZ en FGX.
Viète beweerde dat de onderste twee driehoeken rechthoekig zijn.
| a
| Bereken voor de drietallen (3,4,5) en (5,12,13) de bijbehorende drietallen.
| | b
| Laat zien dat de bijbehorende driehoeken rechthoekig zijn.
| | c
| Bewijs met de stelling van Pythagoras dat voor ieder paar Pythagoreïsch drietallen (b,d,z) en (f,g,x)
ook de drietallen (bg+df,bf−dg,zx) en (bg−df,bf+dg,zx) Pythagoreïsch drietallen zijn.
|
| | Opdracht 3
| Hieronder staan vier driehoeken. Toon aan dat alle driehoeken rechthoekig zijn als geldt dat a² + b² = c².
| |
|
|


  origineel origineel


  origineel origineel
|
|
|
|
hoogtelijn deelt overstaande
44 verso
|
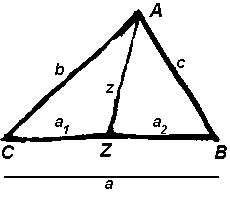
Driehoeken waarvan de hoogtelijn de overstaande zijde in twee geheeltallige stukken deelt
|
Gezocht wordt naar geheeltallige driehoeken waarvan de hoogtelijn de overstaande zijde in twee geheeltallige stukken deelt.
|
GN108
Frans van Schooten tekende driehoeken waarvan de hoogtelijn de overstaande zijde in twee stukken deelde met geheeltallige lengte.
De driehoeken bovenaan waren voor Frans Junior een manier om verschillen van kwadraten uit te drukken.
De linker driehoek drukte uit dat 9² − 7² = 32 maar ook dat 6² − 2² = 32.

Voorbeeld

In dit voorbeeld is:
p = 9 + 7 = 16
q = 9 − 7 = 2
r = 6 + 2 = 8
s = 6 − 2 = 4
h² = 16 × 2 = 8 × 4 = 32
In dit voorbeeld is de hoogtelijn niet geheeltallig, maar de stukken waarin de overstaande zijde verdeeld wordt zijn dat wel!
|
Aanpak
Hiernaast staat ∆ABC met zijden x, y, v en w en hoogtelijn h
en de punten A, B, C en D.
De rechthoekige driehoeken zijn dan ∆ABD en ∆ACD.
Als je wilt weten of er voor zekere hoogte een geheeltallige driehoek bestaat die aan de voorwaarden voldoet,
dan kun je allerlei combinaties van x, y, v en w uitproberen,
maar het kan ook veel slimmer.
Eerst gebruik je de stelling van Pythagoras, herleid je de vergelijkingen, introduceer je nieuwe onbekenden die makkelijker op te lossen zijn
en pas dan los je het feitenlijke probleem op.
Vergelijkingen
Conclusie
Conclusie is dat door slim getallen te kiezen,
de lengten van de zijden berekend kunnen worden van een geheeltallige driehoek waarvan de hoogtelijn de overstaande zijde in twee geheeltallige stukken deelt.
 Recept voor een geheeltallige driehoek waarvan de hoogtelijn de overstaande zijde in twee geheeltallige stukken deelt. Recept voor een geheeltallige driehoek waarvan de hoogtelijn de overstaande zijde in twee geheeltallige stukken deelt.
|
Vierhoeken
Op dezelfde manier stelde Frans van Schooten vierhoeken samen uit geheeltallige rechthoekige driehoeken.
Onderstaande vierhoeken staan op folio 47 recto.
|
 top top
Recept
Met deze vergelijkingen is een recept gemaakt om
driehoeken te maken waarvan de hoogtelijn de overstaande zijde in twee geheeltallige stukken deelt.
 Recept Recept
Lijsten
Het gaat hier om gelijke verschillen van kwadraten:
h² = v² − z²
h² = x² − (y+z)²
y² − x² = w² − v²
Lijsten met gelijke verschillen van kwadraten staan op een aparte webpagina.
 Lijsten Lijsten
|
hoogtelijn snijdt verlengde overstaande
47 recto
|
Driehoeken waarvan de hoogtelijn buiten de driehoek valt en het verlengde van de overstaande zijde geheeltallig is
|
Gezocht wordt naar een geheeltallige driehoek waarvan de hoogtelijn buiten de driehoek valt en het verlengde van de overstaande zijde geheeltallig is.
|
GN108
|
Conclusie
Conclusie is dat door slim getallen te kiezen,
de lengten van de zijden berekend kunnen worden van een geheeltallige driehoek waarvan
de hoogtelijn buiten de driehoek valt en het verlengde van de overstaande zijde geheeltallig is.
 Recept voor een geheeltallige driehoek
waarvan de hoogtelijn buiten de driehoek valt en het verlengde van de overstaande zijde geheeltallig is. Recept voor een geheeltallige driehoek
waarvan de hoogtelijn buiten de driehoek valt en het verlengde van de overstaande zijde geheeltallig is.
|
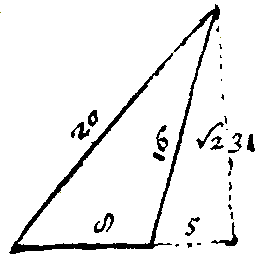
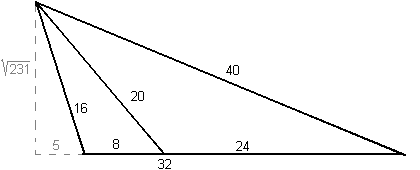
Voorbeeld
Als voorbeeld wordt de schets linksboven doorgerekend.
v = 16, z = 5,
x = 40, y = 32 en y + z = 37.
p = 16 + 5 = 21
q = 16 − 5 = 11
r = 40 + 32 + 5 = 77
s = 40 − 32 − 5 = 3
h² = 21 × 11 = 77 × 3 = 231
Opdracht
Vind alle driehoeken met h = 231.
Opdracht
Het getal 240 laat zich ontbinden in verschillende factoren:
240 = 2 × 120 = 4 × 60 = 6 × 40 = 8 × 30 = 10 × 24
= 12 × 20.
Toon aan dat er 15 mogelijkheden zijn om een geheeltallige driehoek ACD te maken met hoogtelijn h = √‾‾‾240.
|
|
|
hoogtelijn abc
47 recto
|
abc-tje voor geheeltallige driehoeken waarvan de hoogtelijn de overstaande zijde in twee geheeltallige stukken deelt
|
Gezocht wordt naar een abc-tje voor geheeltallige driehoeken waarvan de hoogtelijn de overstaande zijde in twee geheeltallige stukken deelt.
|
GN108
|
In de schets hieronder tekende Frans van Schooten een driehoek en schreef de lengte van de zijden erbij.
Ook tekende hij de hoogtelijn en schreef de lengte erbij: 2abc.
Een hoogtelijn uit een hoek staat altijd loodrecht op de zijde tegenover die hoek.
Dat betekent dat iedere hoogtelijn een driehoek verdeelt in twee rechthoekige driehoeken.
Het linkerdeel van die driehoek is een rechthoekige driehoek met
hoogtelijn 2abc,
rechthoekszijde aac−bbc
en lange zijde aac+bbc.
Het rechterdeel is ook een rechthoekige driehoek met dezelfde hoogtelijn,
met rechthoekszijde abb−acc
en lange zijde abb+acc.
Opdrachten
Opdracht 1:
| Bereken de lengten van de zijden van de rechthoekige driehoeken
voor a = 3, b = 2 en c = 1.
| Opdracht 2:
| Laat met een berekening zien dat volgens de stelling van Pythagoras beide driehoeken rechthoekig zijn.
| Opdracht 3:
| Bewijs met algebra aan dat volgens de stelling van Pythagoras voor iedere a, b en c de driehoeken rechthoekig zijn.
 Antwoord Antwoord
|
Mathematische Oeffeningen
Frans van Schooten legde op bladzijde 397 en 398 van het vijfde boek van de "Mathematische Oeffeningen" uit hoe hij met dit abc-tje geheeltallige driehoeken maakte waarvan de hoogtelijn de overstaande zijde in twee geheeltallige stukken deelde.
 Mathematische Oeffeningen bladzijde 397 en 398 Mathematische Oeffeningen bladzijde 397 en 398
|


NB: Het = teken in de schets betekent aftrekken: −
|
|
| 
|
|
 top top
Notatie
Het = teken in de schets betekent aftrekken: −
Voor het "is gelijk aan" teken gebruikt Frans van Schooten een omgekeerde œ drukletter:  . .
Lees "A history of mathematical notations" van Florian Cajori over de ontwikkeling van de wiskundige notaties.
 Google Books Google Books
Driehoeksongelijkheid
De driehoeksongelijkheid zegt dat de kortste afstand tussen twee punten altijd een rechte lijn is.
Iedere omweg is dus langer.
 Wikipedia: Driehoeksongelijkheid Wikipedia: Driehoeksongelijkheid
|
hoogtelijn deelt overstaande
opera 39
|
bdz-tje voor geheeltallige driehoeken waarvan de hoogtelijn de overstaande zijde in twee geheeltallige stukken deelt
|
Gezocht wordt naar geheeltallige driehoeken waarvan de hoogtelijn de overstaande zijde in twee geheeltallige stukken deelt.
|
Viète Opera Mathematica
Op bladzijde 39 tekende Frans van Schooten in "Viète Opera Mathematica" een rechthoekige driehoek met rechthoekszijden b, d en langste zijde z. Hij beweerde dat de hoogtelijn in driehoek met zijden zb, zd, en b²+d² geheeltallig is en de overstaande zijde in twee gehele stukken deelt.
Opdracht
Toon aan dat voor ieder pythagorees drietal (b,d,z)
de driehoek met zijden zb, zd, en b²+d²
de hoogtelijn geheeltallig is en de overstaande zijde in twee geheeltallige stukken deelt.
|
 
|
|
|
drie hoogtelijnen met hoogtepunt binnen
44 verso
|
Driehoeken met drie geheeltallige hoogtelijnen die ieder de overstaande zijde in twee geheeltallige stukken delen
|
Gezocht wordt naar geheeltallige driehoeken met drie geheeltallige hoogtelijnen waarvan het hoogtepunt binnen de driehoek ligt.
|
GN108
|
Hiernaast staat een driehoek met drie geheeltallige hoogtelijnen die ieder de overstaande zijden in geheeltallige stukken delen
en waarvan het hoogtepunt binnen de driehoek ligt.
Oppervlakte
In iedere geheeltallige driehoek met een geheeltallige hoogtelijn zijn de andere twee hoogtelijnen ook geheeltallig of te schrijven als een breuk.
Dat komt omdat de oppervlakte O van iedere driehoek ABC met zijden a, b en c gelijk is aan het halve produkt van basis en hoogte h.
Dit geldt voor alle drie de hoogtes:.
O = ½ a × hA
O = ½ b × hB
O = ½ c × hC
Dat betekent dat er altijd een geheeltallige vergroting is van die driehoek waarvan alle drie de hoogtelijnen geheeltallig zijn.
Voorbeelden
Hieronder staan voorbeelden, op volgorde van oppervlakte.
Geselecteerd zijn alle driehoeken waarvan alle zijden kleiner dan 1000 zijn.
Opvallend veel driehoeken zijn gelijkzijdig.
|
| | a | b | c | ha | hb | hc |
|
|
|
|
|
| | 25 | 25 | 30 | 24 | 24 | 20
| | 130 | 169 | 169 | 156 | 120 | 120
| | 272 | 289 | 289 | 255 | 240 | 240
| | 350 | 625 | 625 | 600 | 336 | 336
| | 625 | 975 | 1000 | 936 | 600 | 585
| | 845 | 910 | 975 | 840 | 780 | 728
| |
Hieronder staan voorbeelden met een rechte hoek in punt C.
| | a | b | c | ha | hb | hc |
|
|
|
|
|
| | 15 | 20 | 25 | 20 | 15 | 12
| | 65 | 156 | 169 | 156 | 65 | 60
| | 136 | 255 | 289 | 255 | 136 | 120
| | 175 | 600 | 625 | 600 | 175 | 168
| | 580 | 609 | 841 | 609 | 580 | 420
|
Opdrachten
Opdracht 1:
|
Bestudeer deze driehoeken met Geogebra.
 Start Geogebra Start Geogebra
|
Opdracht 2:
|
Bewijs dat er geheeltallige driehoeken bestaan waarvan de hoogtelijn niet geheeltallig is.
|
Opdracht 3:
|
Bewijs dat als in een geheeltallige driehoeken één hoogtelijn niet geheeltallig is, dat dan ook de andere hoogtelijnen niet geheeltallig zijn.
|
Opdracht 4:
|
Bewijs dat er geen enkele geheeltallige gelijkzijdige driehoek bestaat met een geheeltallige hoogtelijn.
|
| 

|
|
|
drie hoogtelijnen met hoogtepunt buiten
44 verso
|
Driehoeken met drie geheeltallige hoogtelijnen die ieder de overstaande zijde in twee geheeltallige stukken delen
|
Gezocht wordt naar geheeltallige driehoeken waarvan ieder van de drie hoogtelijn de overstaande zijde in twee geheeltallige stukken deelt
en waarvan het hoogtepunt buiten de driehoek ligt.
|
GN108
In iedere geheeltallige driehoek met een geheeltallige hoogtelijn zijn de andere twee hoogtelijnen ook geheeltallig of te schrijven als een breuk.
Voorbeelden
Hieronder staan voorbeelden, op volgorde van oppervlakte.
Geselecteerd zijn alle driehoeken waarvan alle zijden kleiner dan 1000 zijn.
Opvallend veel driehoeken zijn gelijkzijdig.
|
| | a | b | c | ha | hb | hc
|
|
|
|
|
|
| | 25 | 25 | 40 | 24 | 24 | 15
| | 35 | 75 | 100 | 60 | 28 | 21
| | 169 | 169 | 312 | 120 | 120 | 65
| | 289 | 289 | 510 | 240 | 240 | 136
| | 275 | 625 | 750 | 600 | 264 | 220
| | 260 | 845 | 975 | 780 | 240 | 208
|
|
|
zwaartelijn
45 recto
|
Driehoeken met geheeltallige zwaartelijn
|
Gezocht wordt naar geheeltallige driehoeken met een geheeltallige zwaartelijn.
|
GN108
In GN108 staan ook een paar zwaartelijnen.
Een zwaartelijn verdeelt per definitie de zijde van deze driehoek in twee evenlange delen.
De zwaartelijn in een driehoek met zijden met lengte 17 en 19 en 20 verdeelt de basis in twee stukken met lengte 10 en 10.
Deze zwaartelijn is exact 15 lang.
De zwaartelijn in een driehoek met zijden met lengte 17 en 19 en 30 verdeelt de basis in 15 en 15.
Deze zwaartelijn is echter niet exact 12 lang, maar exact 10!
Bachet
Tussen de driehoeken staat in GN108 de naam van Bachet en de afkorting Dioph. en "p 418".
Op bladzijde 418 van dat boek wordt inderdaad gerekend aan zwaartelijnen.
Beide voorbeelden staan daar uitgewerkt: de driehoek met zijden 19, 17, 20 en hoogtelijn 15 en de driehoek met zijden 19, 17, 30 en hoogtelijn 12.
Het lijkt erop dat Frans van Schooten het niet heeft nagerekend!
Vergelijkingen
In driehoek ABC met zijden a, b en c is de lengte van de zwaartelijn uit hoek A te berekenen met de volgende formule:
Za² = ½b² + ½c² − ¼a²
Voorbeeld
Reken maar na: 15² = ½×19² + ½×17² − ¼20²
Hieronder staat de berekening van de zwaartelijn met hulp van de bijbehorende hoogtelijn.
Hoogtelijn met hoogte h verdeelt basis in 10 + x en 10 − x.
| (10+x)² + h² = 19² | dus: | 100 + 20x + x² = 361 |
| (10-x)² + h² = 17² | dus: | 100 − 20x + x² = 289
|
Dit stelsel vergelijkingen kan herschreven worden:
100 + x² = 361 − 20x = 289 + 20x
zodat 40 x = 72.
en heeft als oplossing x = 72/40
zodat h² = 354816 / 40² = 221,76
De zwaartelijn is nu 15 want x² + h² = 3,24 + 221,76 = 225 = 15²
Conclusie
Conclusie is dat (deze tekst is nog niet af).
|
 top top
Euclides VI-3
Propositie VI-3 beweert dat een bissectrice van een driehoek de overstaande zijden in stukken deelt die zich verhouden als de zijden die de hoek insluiten.
 propositie VI-3 propositie VI-3
|
deellijn in rechthoekige driehoek
|
Rechthoekige driehoeken met een geheeltallige deellijn die de overstaande zijde in twee geheeltallige stukken deelt
|
Gezocht wordt naar geheeltallige rechthoekige driehoeken waarvan een geheeltallige deellijn de overstaande zijde in twee geheeltallige stukken deelt.
|
GN108
Deze driehoek staat niet in GN108, maar had er zeker niet misstaan.
Dit probleem komt uit het boek "Diophante Arithmeticorum libri sex" van Bachet.
Vergelijkingen
|
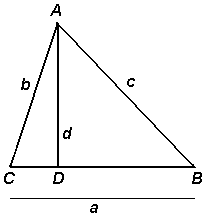
In iedere driehoek ABC met zijden a, b en c
en met deellijn AD van hoek A geldt dat:
|
BD |
= |
CD |
⇔ |
BD |
= |
AB |
⇔ |
BD × AC = CD × AB |
|
|
AB |
AC |
CD |
AC |
|
De suggestie van Bachet in probleem 6-18 is om te beginnen met een Pythagorees drietal (p,q,r) en een onbekende x.
In de tekening hiernaast staan de zijden en hun lengtes.
Met algebra kan dit herschreven worden tot:
c = q − qx want
| CD | =
| px | =
| p
| x | =
| p
| 1 − x | =
| p − px | =
| BD
| | AC
| qx
| q
| x
| q
| 1 − x
| q − qx
| AB
| |
|
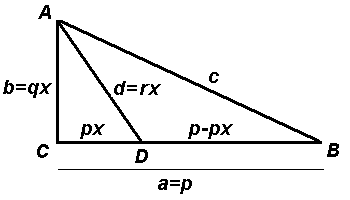
Volgens de stelling van Pythagoras geldt
p² + (qx)² = (q − qx)²
= q² − 2q²x + (qx)²
| 
| |
Na substitutie ontstaan nieuwe vergelijkingen voor a, b, c en d met breuken.
Door deze te vermenigvuldigen met 2q² ontstaan geheeltallige oplossingen voor a, b, c en d.
Conclusie is dat gegeven een Pythagorees drietal (p,q,r),
er een geheeltallige driehoek ABC is met geheeltallige deellijn AD
die zijde BC in twee geheeltallige stukken deelt.
- a = 2pq²
- b = q(q² − p²)
- c = q(q² + p²)
- d = r(q² − p²)
- BD = p(q² + p²)
- CD = p(q² − p²)
|
Voorbeeld
Bij het Pythagorees drietal (p,q,r) = (7,24,25) hoort
a = 8064, b = 12648, c = 15000, d = 13175
en de overstaande zijde is verdeeld in twee stukken ter lengte 3689 en 4375.
 Recept Geheeltallige Deellijn Recept Geheeltallige Deellijn
| |
|
|
 top top
Fragmenten
Klik op de duimnagels voor een vergroting van de relevante tekstfragmenten.

 Bachet: bladzijde 407 Bachet: bladzijde 407
Recept
Maak met het Griekse recept een geheeltallige rechthoekige driehoek waarvan een geheeltallige deellijn de overstaande zijde in twee geheeltallige stukken deelt.
 Geheeltallige Deellijn Geheeltallige Deellijn
|
deellijn
47 recto
|
Driehoeken met een geheeltallige deellijn die de overstaande zijde in twee geheeltallige stukken deelt
|
Gezocht wordt naar geheeltallige driehoeken waarvan een geheeltallige deellijn de overstaande zijde in twee geheeltallige stukken deelt.
|
GN108
Deze driehoeken zijn beslist niet op schaal!
Volgens propositie 3, zesde boek van Euclides, deelt een bissectrice van een driehoek de overstaande zijden in stukken die zich verhouden als de zijden die de hoek insluiten. De overstaande zijde is 80 lang en de zijden zijn 80 en 20 lang.
De overstaande is in de verhouding 80 : 20 verdeeld in 64 en 16.
Vergelijkingen
|
In iedere driehoek ABC met zijden a, b en c
en met AD de deellijn van hoek A geldt dat:
| BC |
= |
CD |
⇔ |
AC |
= |
AB |
⇔ |
AC × BD = CD × AB |
| AB |
BD |
CD |
BD |
| 
| |
Een geheeltallige driehoek met een geheeltallige deellijn die de overstaande zijde in twee geheeltallige stukken deelt,
kan gevonden worden door slim getallen v, w, p, q, r en s te kiezen.
In de tekening hiernaast staat driehoek ABC met zijden:
| a = q × s + q × r
| b = p × s
| c = p × r
|
Daarbij is p = v + w en q = v − w.
Theorema van Stewart
Volgens het theorema van Stewart geldt in iedere driehoek ABC met D op BC:
AD² × BC = AB² × CD + AC² × BD − BC × CD × BD
Substitutie van BD en CD geeft een nieuwe vergelijking voor AD²:
AD² = AB × AC − BD × CD
Driehoeksongelijkheid
In iedere driehoek zijn twee zijden, willekeurig welke, altijd samen langer dan de andere zijde.
Uit deze driehoeksongelijkheid volgt dat:
Conclusie
Conclusie is dat door slim v, w, p, q, r en s te kiezen,
de zijden berekend kunnen worden van een geheeltallige driehoek waarvan de deellijn de overstaande zijde in twee geheeltallige stukken deelt.
 Recept voor een geheeltallige driehoek
waarvan de deellijn de overstaande zijde in twee geheeltallige stukken deelt. Recept voor een geheeltallige driehoek
waarvan de deellijn de overstaande zijde in twee geheeltallige stukken deelt.
|
Voorbeeld
 In de driehoek hiernaast is a = 80, b = 80, c = 20
en AD = 24.
Dat is een vergroting van de driehoek met a = 40, b = 40, c = 10
en AD = 12, BD = 8, CD = 32.
In dat geval is r = 1 en s = 4, v = 9 en w = 1,
zodat p = 10 en q = 8.
Deze getallen horen bij de driehoek met a = 40.
Ook deze driehoek is een vergroting. De kleinste geheeltallige driehoek heeft a = 20, b = 20, c = 5
en AD = 6, BD = 4, CD = 16.
Bij deze driehoek zijn geen geheeltallige r, s etc. te vinden.
In de driehoek hiernaast is a = 80, b = 80, c = 20
en AD = 24.
Dat is een vergroting van de driehoek met a = 40, b = 40, c = 10
en AD = 12, BD = 8, CD = 32.
In dat geval is r = 1 en s = 4, v = 9 en w = 1,
zodat p = 10 en q = 8.
Deze getallen horen bij de driehoek met a = 40.
Ook deze driehoek is een vergroting. De kleinste geheeltallige driehoek heeft a = 20, b = 20, c = 5
en AD = 6, BD = 4, CD = 16.
Bij deze driehoek zijn geen geheeltallige r, s etc. te vinden.
|
Opdrachten
| Opdracht 1:
| Toon met algebra de driehoeksongelijkheden aan.
| | Opdracht 2:
| Toon met algebra aan dat AD = 2√‾‾‾‾rsvw.
| | Opdracht 3:
| Bedenk een recept om slim getallen te vinden voor v, w, p, q, r en s.
 Recept Recept
|
|
 top top
Bachet
Tussen de driehoeken schreef Frans van Schooten in GN108 "Dese 3 triangels heb ick uit Bachetis in Diophanti genomen".
Hieronder staan de relevante passages van bladzijde.
Stewart
M. Stewart was een Schots wiskundige die het theorema in 1746 als eerste zo formuleerde.
Voor hem was deze propositie ook al bekend.
Sommige auteurs verwijzen naar Appolonius, andere naar Archimedes.
 Wikipedia: Formule Wikipedia: Formule
Driehoeksongelijkheid
De driehoeksongelijkheid zegt dat de kortste afstand tussen twee punten altijd een rechte lijn is.
Iedere omweg is dus langer.
 Wikipedia: Driehoeksongelijkheid Wikipedia: Driehoeksongelijkheid
|
omtrek
403
|
Gelijkbenige driehoeken met zelfde omtrek en oppervlakte
|
Gezocht wordt naar geheeltallige gelijkbenige driehoeken waarvan de omtrekken even lang zijn en de oppervlaktes even groot.
|
Mathematische Oeffeningen
|
|
Recepten om geheeltallige driehoeken te vinden
Met lukraak proberen kun je geheeltallige driehoeken vinden, maar het kan ook systematisch.
De oude Babyloniers hadden al een recept om drietallen te vinden voor rechthoekige driehoeken.
Wie kleitablet Plimpton 322 leest, kan bijna niet tot een andere conclusie komen.
De oude Grieken hadden verschillende recepten. Sommige worden toegeschreven aan Pythagoras, Plato en Euclides.
Diophantus reikt een recept aan om geheeltallige rechthoekige driehoek te vinden met een geheeltallige deellijn.
Ook zijn er recepten voor geheeltallige zwaartelijnen en geheeltallige deellijn in willekeurige geheeltallige driehoek.
|
|
|
Lijsten van geheeltallige driehoeken
|
|
 top top
Priemgetallen
Op bladzijde 366 tot en met 375 van het vijfde boek van de "Mathematische Oeffeningen" heeft Frans van Schooten alle priemgetallen onder de 10000 opgesomd.
 Mathematische Oeffeningen Mathematische Oeffeningen
|

 Wat is een geheeltallige driehoek
Wat is een geheeltallige driehoek Sommige rechthoekige driehoeken zijn geheeltallig, bijvoorbeeld driehoek ABC met rechthoekszijden a = 3 en b = 4 heeft langste zijde c = 5.
Oneindig veel rechthoekige driehoeken zijn niet geheeltallig. De gelijkbenige driehoek met rechthoekszijden a = b = 1
heeft langste zijde c = √
Sommige rechthoekige driehoeken zijn geheeltallig, bijvoorbeeld driehoek ABC met rechthoekszijden a = 3 en b = 4 heeft langste zijde c = 5.
Oneindig veel rechthoekige driehoeken zijn niet geheeltallig. De gelijkbenige driehoek met rechthoekszijden a = b = 1
heeft langste zijde c = √













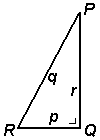






















 .
.