Inhoudsopgave

Dit document is nog lang niet af.
Het hoort onder andere bij fvs_gn108_047rt.htm

Driehoeken met geheeltallige zijden op dezelfde basis en met gelijke hoogte

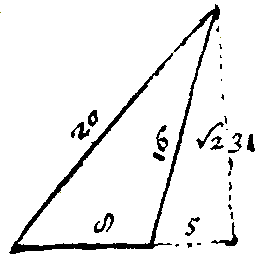
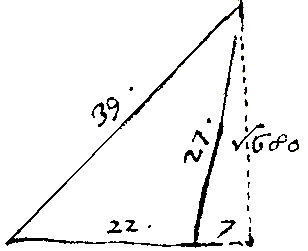
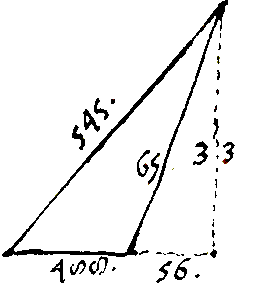
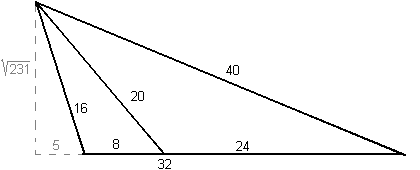
De driehoeken bovenaan zijn voor Frans Junior een manier om een oefening in verschillen van kwadraten uit te drukken. De linker driehoek drukt uit dat 16² − 5² = 231 maar ook dat 40² − 37² = 231. De driehoek daarnaast drukt bovendien uit dat 20² − 13² = 231.
Dat betekent dat onderstaande driehoek bestaat: een driehoek met zijden 16, 32 en 40 met een lijn van 20 die de basis deelt in twee stukken van 8 en 24.

Volgens Goddijn zit hier een slim zoekproces achter. Noem de zijden in de tekening h, v, x, y en z en de punten A, B, C en D. De rechthoekige driehoeken zijn dan ∆ABC en ∆ABD.

Volgens de stelling van Pythagoras geldt:

h² = v² − z²
h² = x² − (y+z)²

Dit zijn merkwaardige producten:

h² = v² − z² = (v − z)(v + z)
h² = x² − (y+z)² = (x − y − z)(x + y + z)

Hier staat dat het verschil van twee kwadraten ook geschreven kan worden als het product van twee getallen.

h² = p × q met p = v − z en q = v + z.
h² = r × s met r = x − y − z en s = x + y + z.

Gevolg is dat ieder getal dat ontbinden kan worden in meer dan drie factoren kandidaat is als hoogte van een samengestelde rechthoekige driehoek. Er is namelijk nog een voorwaarde. De getallen h, v, x, y en z moeten zodanig zijn dat er een driehoek mee te maken is.

h < v < x
v < z + h
x < y + v

Niet iedere factor is kandidaat, want:

h² = p × q met p = v − z en q = v + z.
p + q = 2 × v
q − p = 2 × z

Hieruit volgt dat geheeltallige oplossingen voor v, x, y en z alleen gevonden worden als beide factoren p en q òf even òf oneven zijn. Anders geformuleerd, de som van de factoren p en q moet even zijn

Het getal 240 laat zich ontbinden in een groot aantal factoren.

1 × 240	valt af want samen oneven
2 × 120	geeft z = 59 en v = 61
3 × 80	valt af want samen oneven
4 × 60	geeft z = 28 en v = 32
5 × 48	valt af want samen oneven
6 × 40	geeft z = 17 en v = 23
8 × 30	geeft z = 11 en v = 19
10 × 24	geeft z=7 en v=17
12 × 20	geeft z=4 en v=16
15 × 16	valt af want samen oneven

Hoogtelijn deelt overstaande zijde

In iedere driehoek ABC met zijden a, b en c, met D snijpunt van AC en de hoogtelijn uit B geldt:

	AD =	b² + c² − a²		CD =	b² + a² − c²
		2 × b			2 × b

Merk op dat AD + CD = b.

Als hoek A scherp is, dan is AD positief en ligt de hoogtelijn binnen de driehoek, maar als hoek A stomp is, dan is AD negatief en ligt de hoogtelijn buiten de driehoek.

	BD² = c² − (	b² + c² − a²	)²
		2 × b

Driehoeken met geheeltallige zijden en deellijn

De driehoeken bovenaan heeft Frans van Schooten Junior overgenomen uit Bachet. Daar leest hij over algebraïsche technieken. Volgens Goddijn zit hier een slim zoekproces achter.

Formules

In iedere driehoek ABC met BD de deellijn van hoek B geldt dat:

	AB	=	AD	⇔	AB	=	BC	⇔	AB × CD = AD × BC
	BC		CD		AD		CD

	AD =	AB × AC
	AD =	AB + BC

	CD =	BC × AC
	CD =	AB + BC

BD² = AB × BC − AD × CD

Geheeltallig

Met hulp van een computer zijn een aantal driehoeken gevonden waarvan de lengte van de zijden geheeltallig zijn, de lengte van de deellijn geheeltallig is, evenals de lengte van de stukken waarin de deellijn de overstaande snijdt. Sommige driehoeken zijn een vergroting van elkaar, maar de meeste zijn origineel. Om spiegelingen en rotaties te voorkomen, staan hieronder alleen die driehoeken met AB > BC.

AB	BC	AC	AD	CD	BD
8	6	7	4	3	6
15	12	18	10	8	10
16	12	14	8	6	12
18	9	21	14	7	8
20	5	20	16	4	6
21	14	25	15	10	12
22	11	21	14	7	12
24	18	21	12	9	18
27	15	28	18	10	15
27	24	17	9	8	24
28	16	33	21	12	14
30	24	36	20	16	20
32	24	28	16	12	24
33	22	25	15	10	24
35	28	18	10	8	30
36	18	42	28	14	16
36	28	48	27	21	21
38	19	51	34	17	12
39	13	44	33	11	12
40	10	40	32	8	12
40	24	56	35	21	15
40	30	35	20	15	30