Een diagonaal verdeelt de vierhoek in twee driehoeken met hoogtelijn 12 en 8. De diagonaal is 5 + 10 + 6 = 21 lang. Resultaat is een vierhoek met zijden 17, 10, 20 en 13.
In de bovenste drie rijen toont Frans van Schooten vierhoeken die samengesteld zijn uit vier rechthoekige driehoeken. De onderste rij omvat vier driehoeken met deellijnen. Daartussen staan driehoeken met een algebraïsche notatie.
|
Een diagonaal verdeelt de vierhoek in twee driehoeken met hoogtelijn 12 en 8. De diagonaal is 5 + 10 + 6 = 21 lang. Resultaat is een vierhoek met zijden 17, 10, 20 en 13. | Dezelfde rechthoekige driehoeken zijn anders gerangschikt. Zo ontstaat een vierhoek met zijden 10, 17, 20 en 13. |
|
Een diagonaal verdeelt de vierhoek in twee driehoeken met hoogtelijn 24 en 36. De diagonaal is 10 + 5 + 27 = 42 lang. Resultaat is een vierhoek met zijden 39, 45, 40 en 26. | Dezelfde rechthoekige driehoeken zijn anders gerangschikt. Zo ontstaat een vierhoek met zijden 45, 39, 40 en 26. |
|
Een diagonaal verdeelt de vierhoek in twee driehoeken met hoogtelijn 16 en 36. De diagonaal is 12 + 3 + 27 = 42 lang. Resultaat is een vierhoek met zijden 39, 45, 34 en 20. | Dezelfde rechthoekige driehoeken zijn anders gerangschikt. Zo ontstaat een vierhoek met zijden 39, 45, 20 en 34. |
|
Frans Van Schooten maakte hier slim gebruik van het merkwaardig product.
Links staat een driehoek met hoogtelijn 2abc.
Het linkerdeel van die driehoek is rechthoekig met
rechthoekszijde aac−bbc
en lange zijde aac+bbc.
Het rechterdeel is ook een rechthoekige driehoek met dezelfde hoogtelijn,
met rechthoekszijde abb−acc
en lange zijde abb+acc.
Van Schooten heeft geleerd dat met drie getallen a, b en c een driehoek PQR gemaakt kan worden. De lengte van de hoogtelijn van die driehoek is 2×a×b×c, kort geschreven 2abc. De lengte van de zijden zijn aac−bbc+abb−acc, abb+acc en aac+bbc. De uitwerking van dit merkwaardig produkt en een applet om het effect van a, b en c te aanschouwen staat op een aparte webpagina. NB: Op bladzijde 400 en 401 staan soortgelijke tekeningen waar andere letters gebruikt zijn. |
Na al die rechthoekige driehoeken komt nu iets heel anders. Bij Bachet leest Frans van Schooten Junior over algebraïsche technieken. Hij schreef hier "Dese 3 triangels heb ick uit Bachetis in Diophanti genomen".
| ||
Deze driehoek is beslist niet op schaal. Volgens propositie 3, zesde boek van Euclides, deelt een bissectrice van een driehoek de overstaande zijden in stukken die zich verhouden als de zijden die de hoek insluiten. De overstaande is 80 lang en de zijden zijn 80 en 20. De overstaande is in de verhouding 80 : 20 verdeeld in 64 en 16. Met de stelling van Stewart is de lengte van de deellijn uitgerekend. Die is inderdaad exact 24.
|
|
Volgens propositie 3, zesde boek van Euclides, is een lijn die de overstaande zijde in twee stukken deelt die zich verhouden als de aanliggende zijden een deellijn Omdat 125 : 80 = 100 : 64 is de tophoek inderdaad in twee gelijke hoeken gedeeld. Met de stelling van Stewart is de lengte van de deellijn uitgerekend. Die is inderdaad exact 60.
|
Gelijk het tweede voorbeeld: omdat 640 : 360 = 512 : 288 is de tophoek inderdaad in twee gelijke hoeken gedeeld. Met de stelling van Stewart is de lengte van de deellijn uitgerekend. Die is inderdaad exact 288.
|
|
De getallen uit het derde voorbeeld hebben 8 als grootste gemene deler. Daarom "ofte in de minste getallig" zijn de zijden van de driehoek 100, 45 en 80, de lengte van de deellijn 36 en is de overstaande verdeeld in twee stukken van 64 en 36.
|
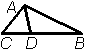
Theorema van StewartHet theorema van Stewart stelt dat in iedere driehoek ABC met D op AC geldt:
M. Stewart was een Schots wiskundige die het in 1746 als eerste zo formuleerde. Voor hem was deze propositie ook al bekend. Sommige auteurs verwijzen naar Appolonius, andere naar Archimedes. | NB: In de laatste figuur zit een gelijkbenige driehoek.
Links Euclides boek 6 propositie 3 Euclides boek 6 propositie 3
 Bachet: Diophante Arithmeticorum libri sex Bachet: Diophante Arithmeticorum libri sex
 Bissectrice stelling Bissectrice stelling
 Stelling van Stewart (1717 - 1785) Stelling van Stewart (1717 - 1785)
|