VII
Van een vierhoekig stuk moeras ABCD zijn de afmetingen bekend:
AB = 58,5 en
BC = 27,3 en
CD = 50,0 en
AD = 32,0.
In het verlengde van AD zijn de punten E en F met
DE = 27,5 en
CE = 32,5.
Gegeven is dat de hoek tussen lijn AF en FC recht is.
Hoe groot is de oppervlakte van vierhoek ABCD?
Notatie
Merk op dat Frans van Schooten de plaats van de komma aangeeft op de manier zoals zijn vader Frans Senior dat overgenomen heeft van Simon Stevin. Het getal 32 met een nul in het rondje betekent dat het getal 32 helen is, maar het getal 275 met een één in het rondje betekent dat het om het getal 27,5 gaat.
Bij de oprichting van de Duytsche Mathematique wordt gewezen op de noodzaak om te rekenen in het tientalligstelsel.

 opdracht 8
opdracht 8

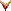 notatie
notatie en 585
en 585  , en bedoelt daarmee 50 eenheden en 585 tienden,
dat wil zeggen 50,0 en 58,5.
Deze notatie is ingevoerd door Simon Stevin in zijn werk "De Thiende".
, en bedoelt daarmee 50 eenheden en 585 tienden,
dat wil zeggen 50,0 en 58,5.
Deze notatie is ingevoerd door Simon Stevin in zijn werk "De Thiende".
 opdracht 6
opdracht 6
 top
top