|
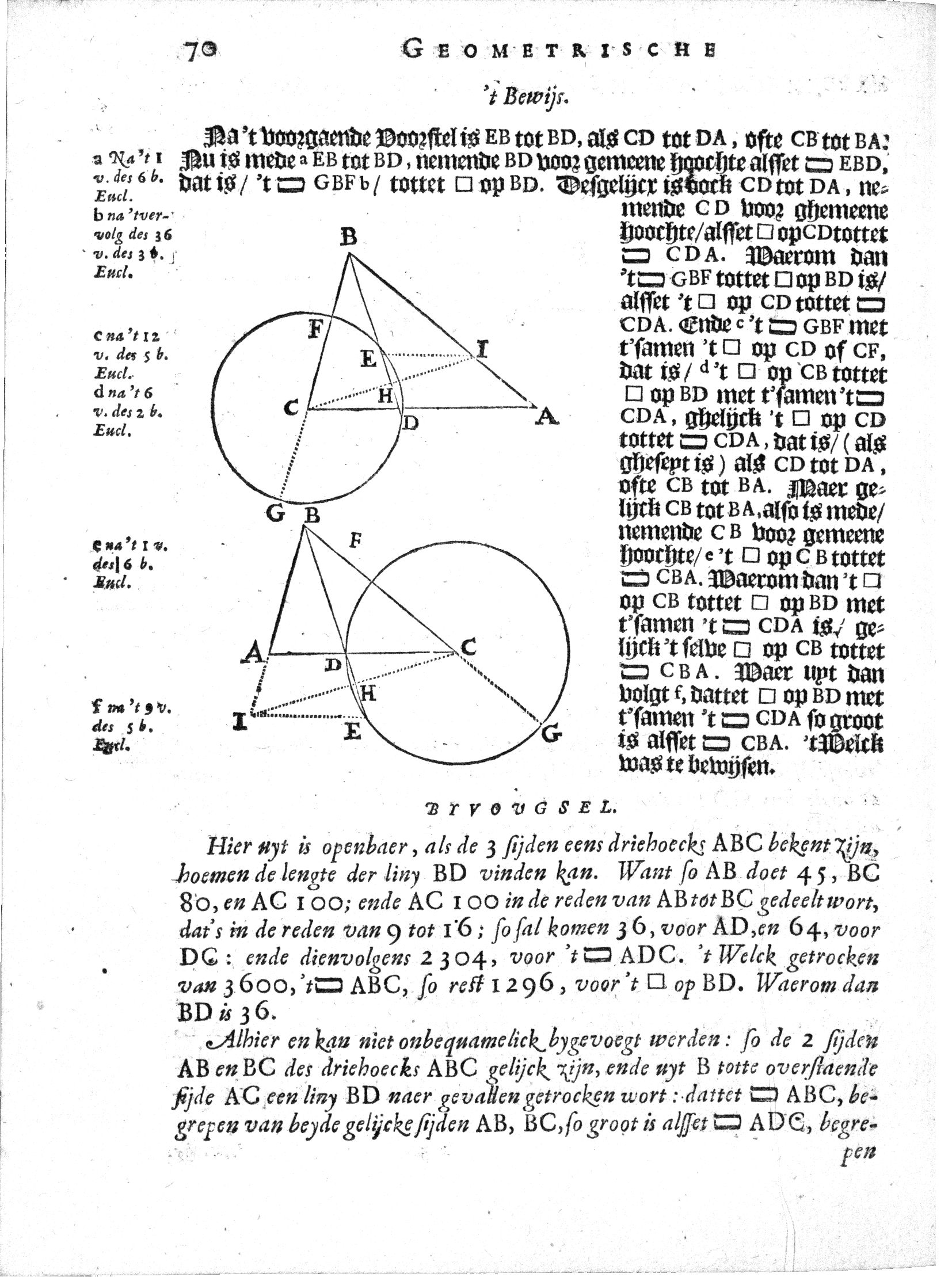
XX Gegeven driehoek ABC, met voetpunt D van de deellijn uit hoek B op zijde AC, met cirkel om punt C door punt D, met punt E, het snijpunt van de cirkel met de deellijn BD, met voetpunt H van de hoogtelijn uit punt C op (het verlengde van) zijde BC, met punt I, het snijpunt van rechte HC met (het verlengde) van zijde AB. Bewijs dat het product van de lengte van de zijden AB en BC gelijk is aan de som van het product van de lengte van de zijden AD en CD en het kwadraat van de lengte van BD. In andere woorden, bewijs dat AB × BC = AD × CD + BD2. |


 rekenvoorbeeld
rekenvoorbeeld opdracht 19
opdracht 19 top
top