www.fransvanschooten.nl

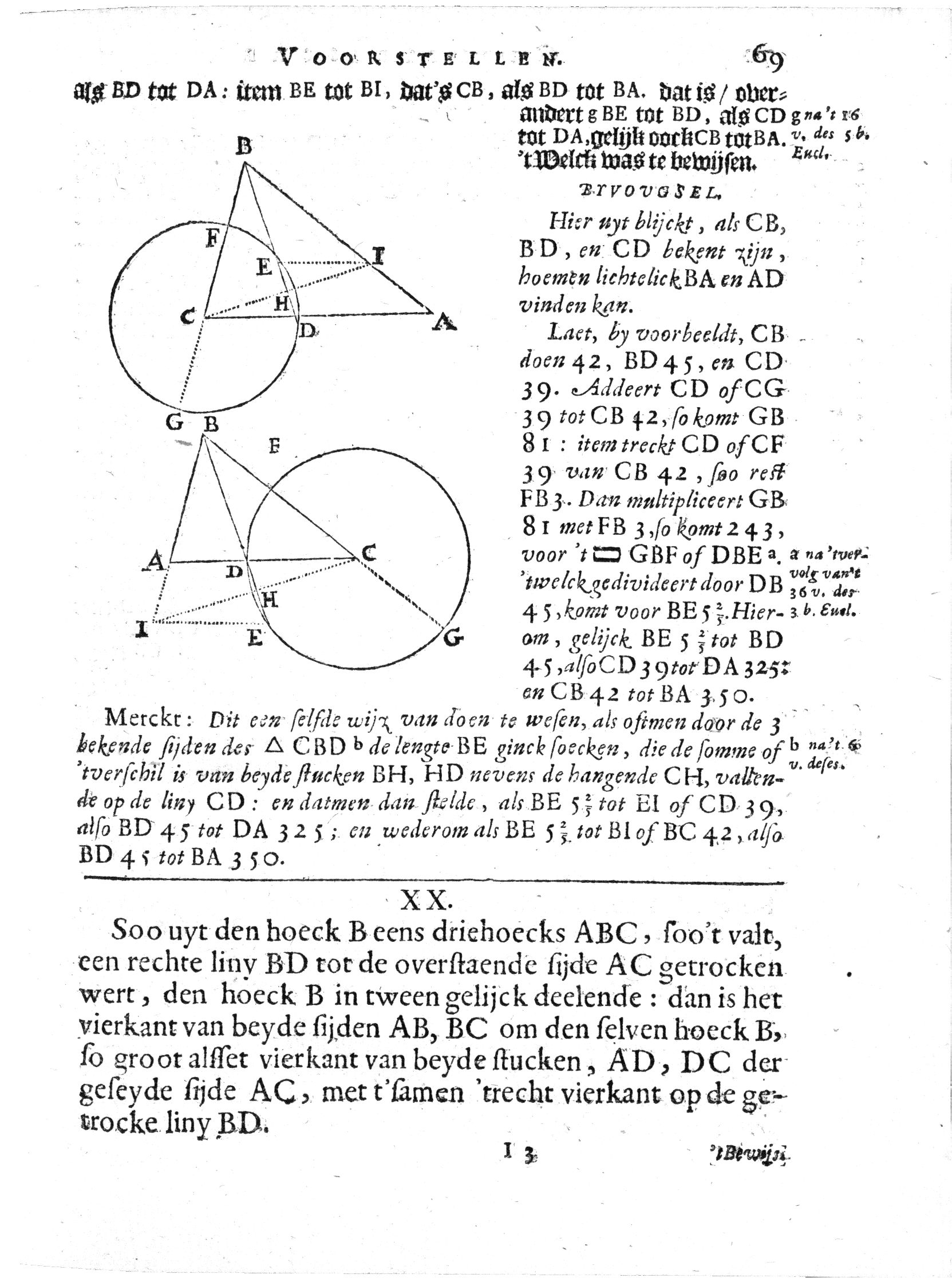
XIX rekenvoorbeeld

Gegeven driehoek ABC, met voetpunt D van de deellijn uit hoek B op zijde AC, met cirkel om punt C door punt D, met punt E, het snijpunt van de cirkel met de deellijn BD, met voetpunt H van de hoogtelijn uit punt C op (het verlengde van) zijde BC, met punt I, het snijpunt van rechte HC met (het verlengde) van zijde AB.

Gegeven is dat BC = 42 en BD = 45 en CD = 39.

Bewezen in opdracht 19 is dat BD : BE = AD : CD = AB : BC.

Bereken de lengte van AB en AD.

tip

  1.   

antwoord machtsstelling

  1.   

    • antwoord machtsstelling

      Te bewijzen is dat AD × CD = FD × GD = BD2.

      Stel AM = BM = CM = r en DM = s,
      dan BD2 = s 2 − r 2 (stelling van Pythagoras)
      dan FD × GD = (s − r) × (s + r) = s 2 − r 2.
      Vanwege de constante hoek op koorde AF is ∠ACF = ∠AGF.
      Vanwege gelijke hoeken is ∆ACK gelijkvormig met ∆FGK.
      Vanwege gelijke hoeken is ∆DFC gelijkvormig met ∆DAG en dus CD : FD = GD : AD oftewel AD × CD = FD × GD.

      Conclusie is dat AD × CD = FD × GD = BD2.


antwoord AB en AD

  1.   

    • antwoord AB en AD

      Omdat BC = 42 en CD = 39 is BF = 42 − 39 = 3 en is BG = 42 + 39 = 81, zodat BF × BG = 3 × 81 = 243.

      Omdat BD = 45 en BF × BG = BE × BD is BE = 5,4.

      Uit
      BD=AD=AB
      BECDBC
      volgt AD = 325 en AB = 350.


bewijs

opdracht 18

opdracht 20

top