|
| ||||
Ellipsograaf van Simon StevinDoor Simon Stevin is een ellipsograaf gemaakt waarmee halve ellipsen getekend kunnen worden. Frans van Schooten behandelt dit op bladzijde 300.
|
| |||
Tuinman's Ellips van Frans van SchootenFrans van Schooten behandelt zijn tuinman's ellips op bladzijde 302.
Plaats de punten H en I, de centra van de ellips, op een willekeurige plaats.
|
| |||
Ellipsograaf van Frans van SchootenFrans van Schooten behandelt zijn tuinman's ellips op bladzijde 318.
Plaats de punten C en F, de centra van de ellips, op een willekeurige plaats.
|
| |||
Parabolograaf van Frans van SchootenOm mechanisch een parabool te tekenen zetten we eerst een lange lat vast op het papier. Deze lat heeft een gleuf waar knop G in bewegen kan. We zetten de parabolograaf vast in punt B, plaatsen een potlood in de kruising van de twee latten met een gleuf. Het apparaat is nu klaar voor gebruik. We bewegen knop G langs de lange lat en het potlood beweegt in de kruising mee en tekent zo de parabool. |
| |||
Hyperbolograaf van Frans van Schooten |
| |||
Heliograaf van NicomedesNicomedes was een wiskundige uit de helleense oudheid, wiens werkzaamheid omstreeks 200 v. C. plaats vond. Hij heeft een kromme gevonden, die bekend staat als conchoïde (schelplijn) |  | |||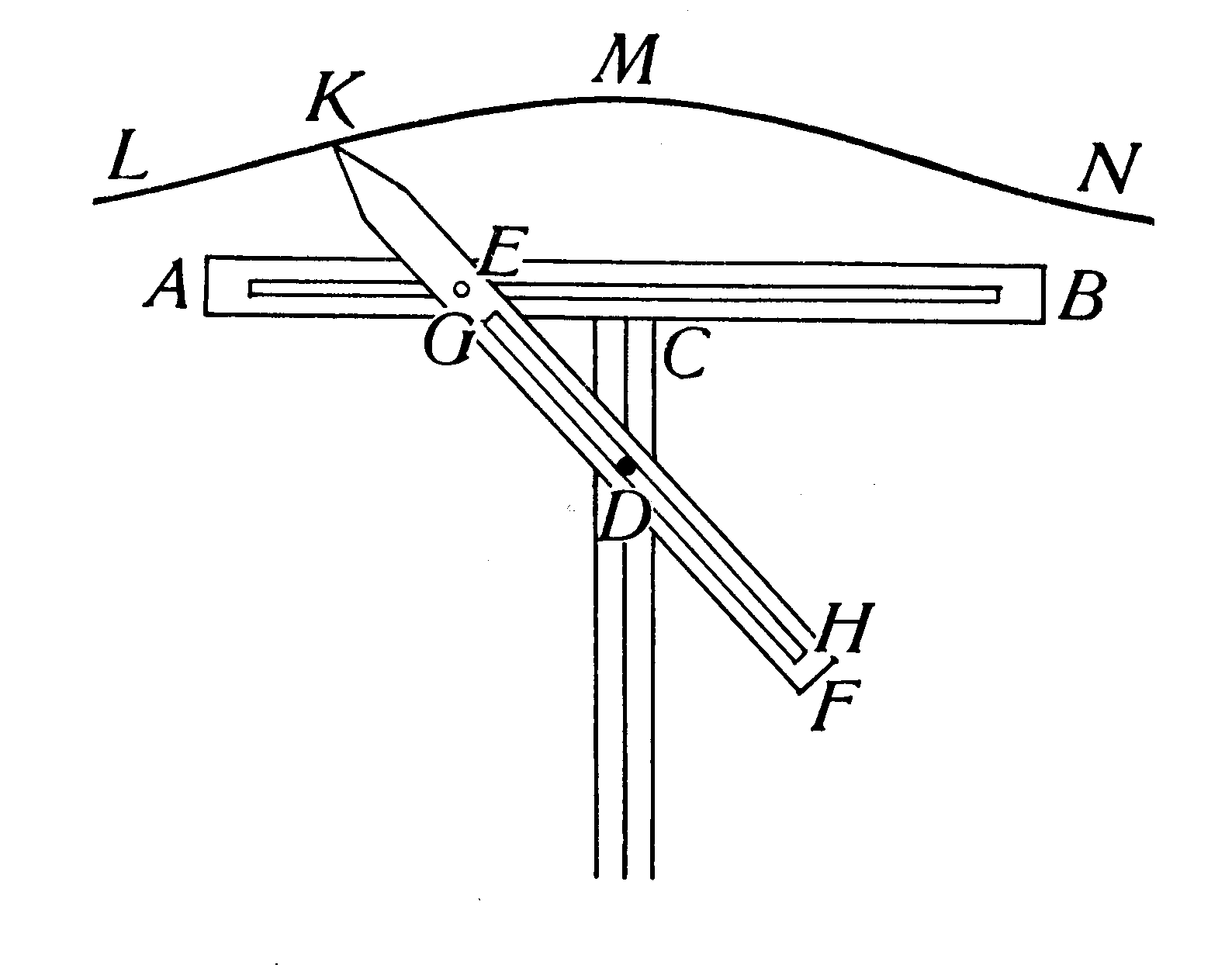
Ellipsograaf van Christiaan HuygensEen versie om lenzen te fabriceren is door Huygens ontwikkeld. Het principe is gebaseerd op de halve ellips van Simon Stevin. Aan de bovenzijde komt het stalen schuurblok en aan de onderkant is de hendel om soepel kracht te zetten voor de schuuractiviteit.De tekeningen zijn ontleend aan een brief van Christiaan Huygens aan Francesco Mocchi, een italiaanse beeldhouwer, gedateerd 1656. |
| |||
|
| ||||
ellipsolograaf
top
grote versie geogebra applet
