Uitwerkingen Hoofdstuk 5 Meetkunde

opdracht T9

De middens van vierhoek ABCD zijn vierhoek PQRS.

opdracht T8

opdracht T4

In de figuur snijden de benen van ∠A en ∠B elkaar in de punten C, F, G en H.
Gegeven is dat ∠A = ∠B.

opdracht T2

Gegeven is een driehoek ABC waarvan de middelloodlijn m van zijde AB snijdt zijde AC in punt D en waarvan punt S het snijpunt is van de middelloodlijn van zijde AB en de deellijn van hoek C.
Bewijs dat ∠DSC = ∠B + ½∠C − 90°

opdracht T1

opdracht 42

opdracht 41

Van vierhoek ABCD snijden de diagonalen AC en BD elkaar in punt S. Gegeven is dat de oppervlakte van ∆ADC gelijk is aan de oppervlakte van ∆ABC.
Bewijs dat punt S het midden is van diagonaal BD.

opdracht 39

Gegeven is driehoek ABC met zwaartelijnen AP en BQ. De zwaartelijnen zijn verlengd tot het dubbele: APR en BQS.
Te bewijzen is dat de punten S, C en R op één lijn liggen.

opdracht 32

Gegeven zijn twee rechthoekige driehoeken, ABC en CDE, waarvan de basis evenwijdige zijn en ook |BC| = |DE|.
Te bewijzen is dat de basishoeken van ∆CAE even groot zijn: ∠CAE = ∠CEA.

opdracht 31

Gegeven is driehoek HPQ, ingesloten door een deellijn en twee hoogtelijnen van driehoek ABC.
Te bewijzen is dat twee zijden van driehoek HPQ even lang zijn.

opdracht 29

Van vierhoek ABCD is punt A het middelpunt van de cirkel en liggen de punten B, C en D op de cirkelrand. Zijde AD is evenwijdig aan zijde BC.
Te bewijzen is dat als vierhoek ABCD een parallellogram is dat het dan een ruit is.

opdracht 28

Het vermoeden dat in driehoek ABC waar de bissectrice van hoek A zijde BC snijdt in punt D tot gevolg heeft dat

|BD|	=	|DC|
|AB|	|AC|

wordt bewezen in opdracht 42.

opdracht 27

Van vierhoek ABCD is ∠B = ∠D = 90° en |AB| = |BC|.
Op het verlengde van zijde DC aan de kant van punt C ligt punt E met |AD| = |CE|.
Te bewijzen is dat |BD| = |BE|.

opdracht 26

Gegeven is parallellogram ABCD.
Bewijs dat de vier deellijnen een rechthoek insluiten.

Bewijs ook dat als van een vierhoek de vier deellijnen een rechthoek insluiten, dat dan de vierhoek een parallellogram is.

opdracht 25

Gegeven zijn hoek A en hoek B waarbij de deellijnen van die hoeken loodrecht op elkaar staan.
Bewijs dat de snijpunten van de benen van de hoeken een ruit vormen.

opdracht 24

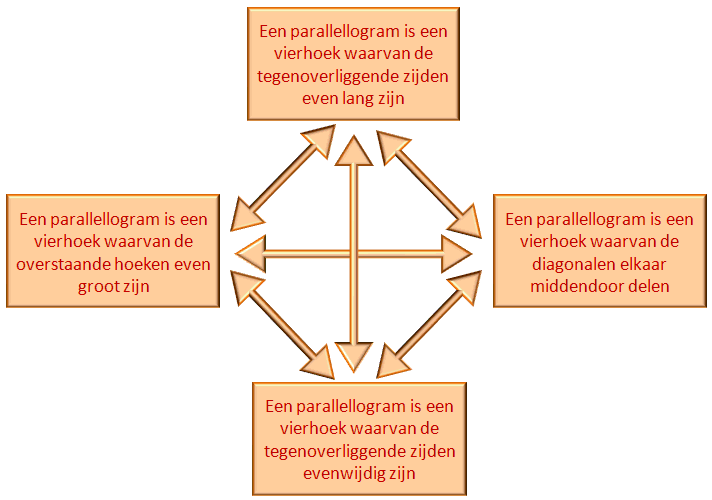
equivalente definities parallellogram

Het boek geeft vier definities van een parallellogram. Die vier definities zijn equivalent: je kunt namelijk vanuit iedere definitie elke andere definitie bewijzen.

opdracht 22

Gegeven is ∆ABC met de zwaartelijnen AD en BE waarbij |AD| = |BE|. Punt S is het snijpunt van de zwaartelijnen.
Bewijs dat ∆ABC gelijkbenig is.

opdracht 21

Vierhoek ABCD is een gelijkbenig trapezium met AB evenwijdig aan CD en |AD| = |BC| Het snijpunt van de diagonalen is S.
Bewijs dat |AC| = |BD|.

opdracht 19

Gegeven is gelijkbenige driehoek ABC met top A. Punt P ligt op de deellijn vam ∠A. Lijn CP snijdt lijn AB in punt R en lijn BP snijdt AC in punt Q waarbij |AD| = |BE|.
Bewijs dat |RB| = |QC|.

opdracht 18

opdracht 12

opdracht 11

opdracht 10

opdracht 9

opdracht 7

opdracht 6

opdracht 5

opdracht 4

voorbeeld

Frans van Schooten
pagina 157

opdracht 157

Frans van Schooten
pagina 122

opdracht 122

Frans van Schooten
pagina 126

opdracht 126