|
Uitwerkingen
De uitwerkingen zijn een co-productie van een docent en een oplettende klas.
|
|
 top top
|
Een logische opbouw
Het boek laat je eerst kennismaken met de stelling van de omtrekshoek, dan met de stelling van de constante hoek en pas daarna met de stelling van de koordenvierhoek. Hieronder staat een andere volgorde.
- Koordenvierhoek te bewijzen met hoekensom (bewijs staat hieronder, zie opdracht 14)
- Thales te bewijzen met een rechthoek (zie opdracht 8)
- Omgekeerde van Thales te bewijzen met gelijkbenige driehoeken (zie opdracht 9)
- Constante hoek te bewijzen met de koordenvierhoek (bewijs staat hieronder)
- Omtrekshoek te bewijzen met de koordenvierhoek (bewijs staat hieronder)
- Omgekeerde van koordenvierhoek te bewijzen met tegenspraak en de koordenvierhoek (zie opdracht 18)
- Omgekeerde van constante hoek te bewijzen met tegenspraak en congruentie (zie opdracht 11)
Op deze manier ontstaat een logische keten van bewijzen die op elkaar voortbouwen.
Koordenvierhoek
Een koordenvierhoek is een vierhoek waarvan de vier hoekpunten op één cirkel liggen.
Van iedere koordenvierhoek is de som van twee overstaande hoeken 180°
Bewijs: Vanuit middelpunt M heeft de koordenvierhoek vier gelijkbenige driehoeken.
In iedere gelijkbenige driehoeken zijn de basishoeken gelijk.
De som van alle acht hoeken is 360°.
∠A + ∠B + ∠C + ∠D = 360°
De som van de vier verschillende basishoeken is 180°.
∠A1 + ∠B1 + ∠C1 + ∠D1 = 180°.
De som van de overstaande hoeken
∠A + ∠C
= ∠A1 + ∠A2 + ∠C1 + ∠C2
= ∠A1 + ∠D1 + ∠C1 + ∠B1
= 180°.
Conclusie is dat van iedere koordenvierhoek de som van twee overstaande hoeken 180° is.
 zie opdracht 14 zie opdracht 14

Omgekeerde stelling koordenvierhoek
Als de som van een paar overstaande hoeken van een vierhoek 180° is, dan is de vierhoek een koordenvierhoek.
 zie opdracht 18 zie opdracht 18
| Constante Hoek
Op een cirkel met opeenvolgende punten A, B en C heeft ieder punt Q tussen A en C dezelfde hoek: ∠AQC = ∠ABC.
Bewijs: Omdat in een koordenvierhoek ∠B + ∠D = 180°
en ook ∠Q + ∠D = 180°
daarom ∠Q = ∠B.
Conclusie is dat bij gelijke koorde AC iedere hoek AQC even groot is.

…,
mits punt Q op dezelfde boog AC is.
Op de formulekaart staat het zo:
Als punt C over een cirkelboog AB tussen de punten A en B beweegt, dan verandert de grootte van de omtrekshoek ACB niet.
Omgekeerde stelling van de constante hoek
Als punt D aan dezelfde kant van AB ligt als punt C en de hoeken ADB en ACB zijn even groot, dan liggen de punten C en D op dezelfde cirkelboog AB.
| Omtrekshoek
Elke omtrekshoek is half zo groot als de bijbehorende middelpuntshoek
Bewijs: in onderstaand, bijzondere geval geldt volgens de stelling van de buitenhoek dat ∠M1 = ∠B2 + ∠C2. Omdat ∠B2 = ∠C2 daarom ∠C2 = ½ ∠M1.
Voor ieder punt Q op de lange boog is volgens de stelling van de constante hoek ∠AQB = ∠ACB.
Conclusie is dat de omtrekshoek half zo groot is als de bijbehorende middelpuntshoek.

NB: Als punt Q niet op de lange boog, maar op de korte boog ligt,
dan is ∠AQB uiteraard niet ½∠M1
maar ∠AQB = 180° − ½∠M1.
Hetgeen te bewijzen is met de stelling van de koordenvierhoek.
|  top top
|
Thales
Als hoek C in ∆ABC recht is,
dan ligt punt C op de cirkel met middellijn AB.
 zie opdracht 8 zie opdracht 8
| Omgekeerde van Thales
Als punt C op de cirkel met middellijn AB ligt,
dan is ∆ABC een rechthoekige driehoek met hoek C recht.
 zie opdracht 9 zie opdracht 9
|
|
 top top
|
opdracht T9

|
uitwerking T-9

|
 top top
|
opdracht T8

|
 top top
|
opdracht T6

|
 top top
|
opdracht T5

|
 top top
|
opdracht T4

|
 top top
|
opdracht T3

|
 top top
|
opdracht T2

|
 top top
|
opdracht 35

|
uitwerking 35
|
 top top
|
opdracht 34

|
uitwerking 34

|
 top top
|
opdracht 33

|
uitwerking 33
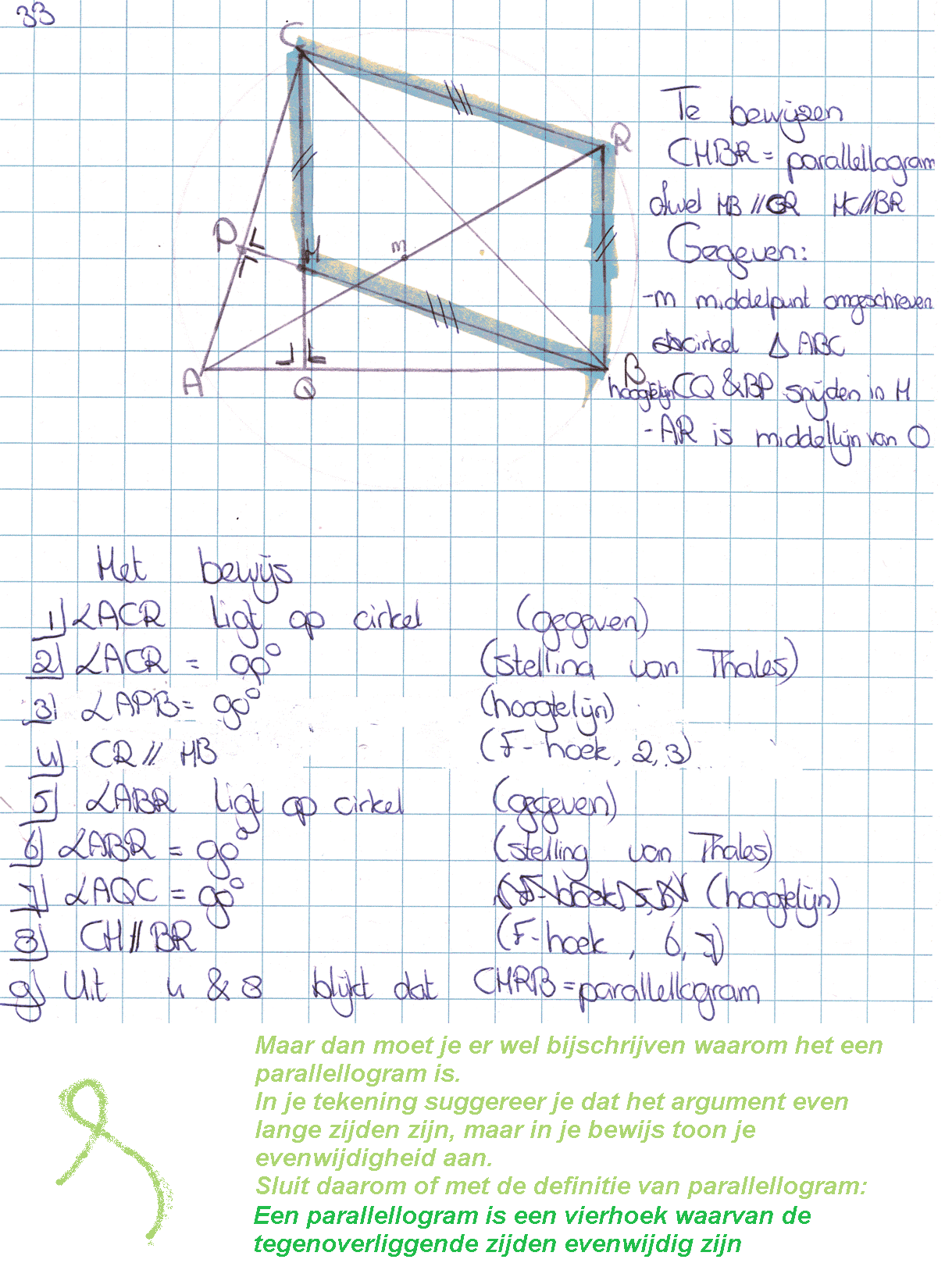
Gegeven is een driehoek ABC met de omgeschreven cirkel met middelpunt M en middellijn AMR.
Punt H is het snijpunt van de hoogtelijn uit punt B en de hoogtelijn uit punt C.
Bewijs dat vierhoek CHBR een parallellogram is.
|
 top top
|
opdracht 32

|
uitwerking 32 c
Gegeven cirkel om middelpunt M en koordenvierhoek ABCD.
Punt P is het snijpunt van de diagonalen AC en BD.
Bewijs dat ∠APB = ½ (∠AMB + ∠CMD).
uitwerking 32 f
Gegeven cirkel om middelpunt M en koordenvierhoek ABCD.
Punt P is het snijpunt van de lijnen AD en BC.
Bewijs dat ∠APB = ½ (∠CMD − ∠AMB).
|
 top top
|
opdracht 31

|
uitwerking 31
Gegeven driehoek ABC met de omgeschreven cirkel met middelpunt M,
en de ingeschreven cirkel met middelpunt I,
en punt D is het snijpunt van de omgeschreven cirkel en de bissectrice van hoek C.
Bewijs dat voor ieder punt C op de omgeschreven cirkel geldt dat de meetkundige plaats van punt I
de cirkel met middelpunt D is door de punten A en B.
|
 top top
|
opdracht 30

|
uitwerking 30
Gegeven driehoek ABC met de omgeschreven cirkel met middelpunt M,
de bissectrices van hoek B en hoek C die elkaar snijden in punt I,
en punt F is het snijpunt van de omgeschreven cirkel en de bissectrice van hoek C.
Bewijs dat |FI| = |FB|.
|
 top top
|
opdracht 29

|
uitwerking 29
Gegeven driehoek ABC met de omgeschreven cirkel met middelpunt M.
Bewijs dat punt S, het snijpunt van de deellijn van ∠C met de middelloodlijn AB,
ligt op de omgeschreven cirkel.
|
 top top
|
opdracht 28

|
uitwerking 28
Gegeven cirkel om middelpunt M en koorde AB
met punten P en Q met |AP| = |BQ|
en snijpunten R en S van de cirkelrand met de lijnen MP en MQ.
Bewijs dat |PR| = |QS|.
|
 top top
|
opdracht 27

|
uitwerking 27
|
 top top
|
opdracht 26

|
uitwerking 26
Gegeven is driehoek ABC met de omgeschreven cirkel met middelpunt M.
Punt D is het midden van zijde BC.
Laat punt C de omgeschreven cirkel doorlopen.
Bewijs dat de meetkundige plaats van punt D een cirkel is.
|
 top top
|
opdracht 25

|
uitwerking 25
Gegeven cirkel met middelpunt M en een punt P binnen die cirkel.
Door punt P gaat een koorde AB met midden S.
Bewijs dat de meetkundige plaats van punt S een cirkel is.
|
 top top
|
opdracht 24

|
uitwerking 24
Gegeven is de omgeschreven cirkel van driehoek ABC met middelpunt M.
De hoogtelijn uit punt A snijdt de overstaande zijde BC in punt D.
Geogebra laat een cirkel zien. De hoogtelijn uit punt A kan zowel binnen als buiten de driehoek vallen.
In Geogebra is dat met kleurtjes aangegeven.
Dat betekent dat je in het bewijs drie gevallen moet onderscheiden om aan te tonen dat de cirkel de meetkundige plaats is van alle punten D die het snijpunt zijn van de hoogtelijn uit punt A en (het verlengde van) de overstaande zijde BC.
|
 top top
|
opdracht 23

|
uitwerking 23
Gegeven is een cirkel met middelpunt M en de punten A en B op de cirkelrand.
Gegeven is ook punt P op de cirkelrand en punt X in het verlengde van lijnstuk BP met |AP| = |XP|.
Te bewijzen is dat voor ieder punt P op de cirkelrand ∠AXP = ½∠APB,
dat alle punten X op cirkels liggen en dat ook de punten A en B op die cirkels liggen.
Met Geogebra krijg je het vermoeden dat afhankelijk van of punt P op de lange of de korte boog is,
punt X op de ene of de andere cirkelboog ligt.
Nu moet je aan gevalsonderscheiding doen.
|
 top top
|
opdracht 22

|
uitwerking 22
Gegeven is driehoek ABC. De hoogtelijn uit punt C snijdt zijde AB in punt D.
De cirkel met middelpunt M en middellijn CD snijdt zijde AC in punt E en zijde BC in punt F.
Bewijs dat vierhoek ABFE een koordenvierhoek is.

|
 top top
|
opdracht 21

|
uitwerking 21
In de gegeven figuur is ∠P = ∠Q = 90°.
Punt T is het midden van lijnstuk AS en punt U is het midden van lijnstuk BS.
Te bewijzen is dat vierhoek TUQP een koordenvierhoek is.
|
 top top
|
opdracht 20

|
|
 top top
|
opdracht 19

|
 top top
|
opdracht 18

|
uitwerking 18
Omdat je de koordenvierhoekstelling al bewezen heb, kun je die nu gebruiken om met tegenspraak te bewijzen
dat als ∠A + ∠C = 180°
dat dan punt D niet buiten of binnen de omgeschreven cirkel van ∆ABC kan liggen,
want ook ∠B + ∠D = 180° (hoekensom vierhoek).
|
 top top
|
opdracht 17
Van vierhoek ABCD gaan de middelloodlijnen van drie zijden door één punt M.
Bewijs dat punt M ook op de middelloodlijn van de vierde zijde ligt.
Bewijs ook dat vierhoek ABCD een koordenvierhoek is.

|
uitwerking 17
Onderzoek eerst met geogebra een "gewone" vierhoek.
Onderzoek daarna de betekenis van de middelloodlijnen voor de punten van de vierhoek.
|
 top top
|
opdracht 14

|
 top top
|
opdracht 13
Voor alle punten P op cirkelboog ACB is ∠APB = γ.
Lijn l is de raaklijn in punt A aan de cirkel.
Punt M is het middelpunt van de cirkel.
|
uitwerking 13
Maak onderscheid tussen een scherpe hoek γ en een stompe hoek.
|
 top top
|
opdracht 11

|
Tegenspraak
Gebruik tegenspraak: er bestaat geen punt Q met ∠ACB = ∠AQB dat niet op de cirkel ligt.
dus liggen alle punten Q met ∠ACB = ∠AQB ALTIJD op de cirkel.
Conclusie: Alle punt Q met ∠ACB = ∠AQB liggen niet buiten, maar op de omgeschreven cirkel van ∆ABC.

|
 top top
|
opdracht 10

|
uitwerking 10
Gebruik de stelling van Thales, de omtrekshoek en de constante hoek.
|
 top top
|
opdracht 9

|
uitwerking 9
Opdracht is de omgekeerde stelling van Thales te bewijzen:
Als punt C op de cirkel met middellijn AB ligt,
dan is ∆ABC een rechthoekige driehoek met hoek C recht.
|
 top top
|
opdracht 8

|
|
uitwerking 8
Opdracht is de stelling van Thales te bewijzen:
Als hoek C in ∆ABC recht is,
dan ligt punt C op de cirkel met middellijn AB.
Een rechthoek heeft een aantal prettige eigenschappen.
 eigenschappen eigenschappen
| 
|
|
 top top
|
opdracht 7

|
De hoek tussen een raaklijn en en koorde is gelijk aan de bij die koorde horende omtrekshoek.

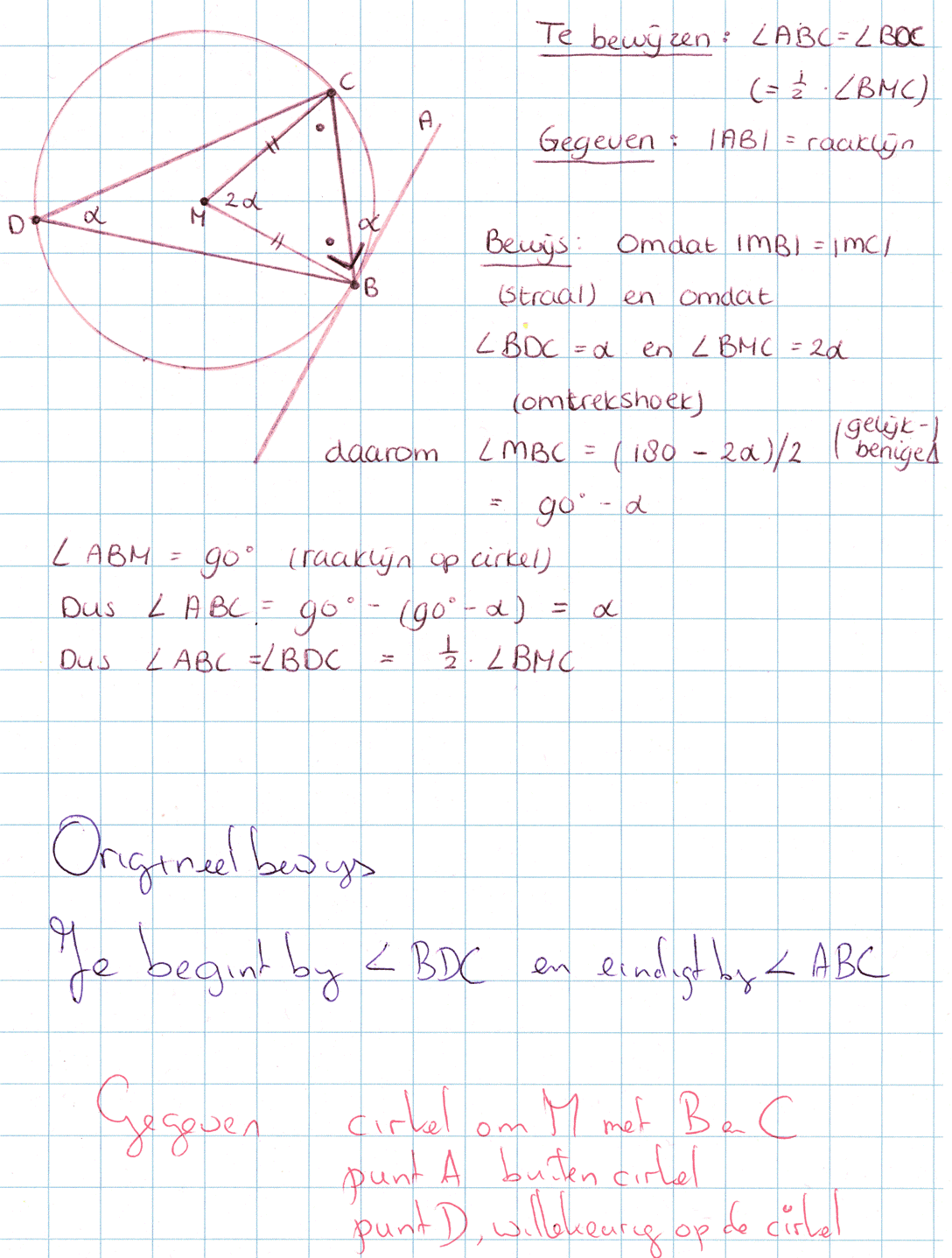
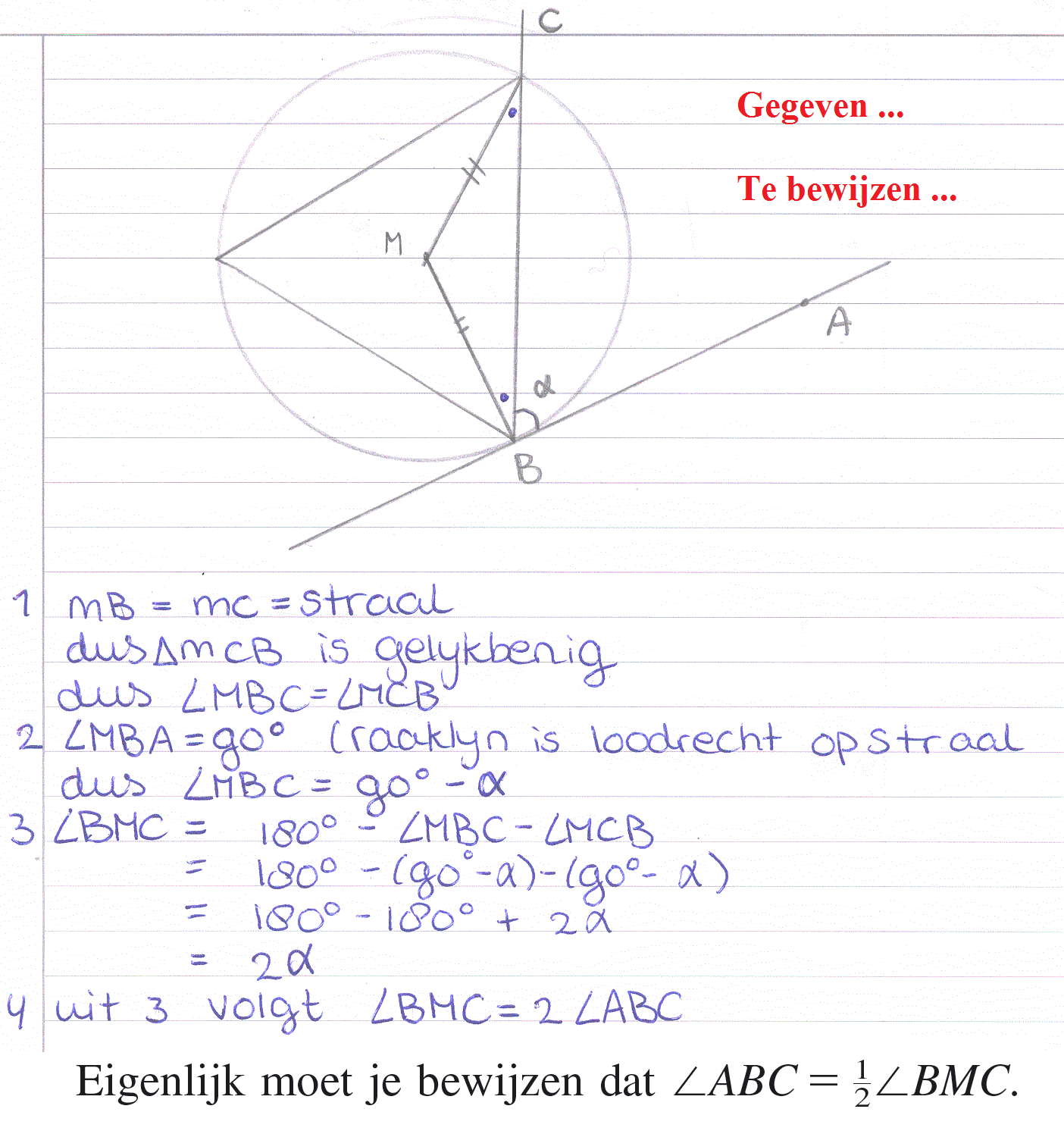

|
 top top
|
|
|
uitwerking 6d
Veronderstel dat een raaklijn aan een cirkel niet loodrecht staat op de verbindingslijn van midden M en raakpunt R.
Die veronderstelling leidt tot tegenspraak.
Met de techniek van tegenspraak kun je bewijzen dat een raaklijn dus altijd loodrecht op de verbindingslijn staat,
want de raaklijn kan niet niet loodrecht staan (let op de dubbele ontkenning).

|
 top top
|
opdracht 5
Twee evenwijdige lijnen snijden een cirkel.
Daartussen worden de bogen AB en CD afgesneden.
|
uitwerking 5a
Omdat lijn AC twee evenwijdige lijnen snijdt,
daarom zijn er Z-hoeken en dus ∠BCA = CAD.
Omdat de omtrekshoeken even groot zijn, zijn ook de middelpuntshoeken even groot.
Omdat de middelpuntshoeken even groot zijn, zijn ook de bogen even groot.
☐
uitwerking 5b
|
 top top
|
opdracht 3

|
|
Elke omtrekshoek is half zo groot als de bijbehorende middelpuntshoek
In een aantal stappen maak je de stelling van de omtrekshoek algemeen.
Mijn uitwerking begint met een bijzonder geval die zich makkelijk laat bewijzen.
Met dat bijzondere geval kun je vervolgens het algemene geval bewijzen.
| 
|
|
 top top
|
opdracht 2

|

